题目内容
11．已知关于x方程3x2+2（1-a）x-a（a+2）=0至少有一实根大于1，则a的取值范围是a＞1或a＜-5．分析 因式分解法求出方程的根x1=a，x2=-$\frac{a+2}{3}$，根据方程至少有一实根大于1可列不等式，解不等式得a的范围．
解答 解：将方程左边因式分解得：（x-a）（3x+a+2）=0，
∴方程的解为：x1=a，x2=-$\frac{a+2}{3}$，
∵方程3x2+2（1-a）x-a（a+2）=0至少有一实根大于1，
∴a＞1或-$\frac{a+2}{3}$＞1，
解得：a＞1或a＜-5，
故答案为：a＞1或a＜-5．
点评 本题主要考查一元二次方程的根的情况，观察方程特点因式分解法表示方程的根是关键，由根的情况列出不等式是根本．
练习册系列答案
相关题目
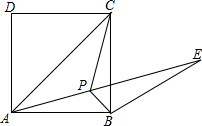如图，已知点P为正方形ABCD内一点，∠BAP=∠BCP=15°．
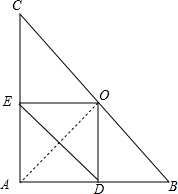如图，在Rt△ABC中，AB=AC，∠BAC=90°，点O为BC的中点，点D，E分别在AB，AC上滑动且保持BD=AE．在滑动过程中△ODE与△ABC会相似吗？会永远相似吗？请说明你的结论．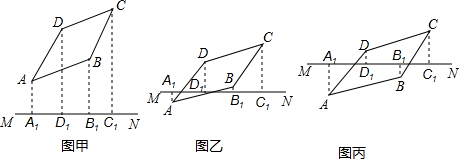
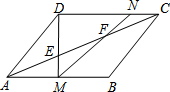平行四边形ABCD中，AB=28，E、F是对角线AC上的两点，且AE=EF=FC，DE交AB于点M，MF交CD于点N．求AM、CN的长．