题目内容
8.若反比例函数y=(k-1)${x}^{{k}^{2}-5}$的图象经过第二、四象限,则k=-2.分析 根据反比例函数的图象在第二、四象限得出k-1<0,且k2-5=-1,由此即可解决问题.
解答 解:由题意$\left\{\begin{array}{l}{k-1<0}\\{{k}^{2}-5=-1}\end{array}\right.$解得k=-2.
故答案为-2
点评 本题考查反比例函数图象的性质、熟练掌握反比例函数的性质是解决问题的关键,记住k>0图象在一、三象限,k<0图象在二、四象限,属于中考常考题型.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
20.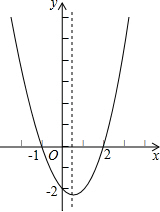 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )| A. | 函数有最小值 | B. | 对称轴是直线x=$\frac{1}{2}$ | ||
| C. | 当x<$\frac{1}{2}$时,y随x的增大而减小 | D. | 当-1<x<3时,y>0 |
17.下列计算,正确的是( )
| A. | 3a2×2a2=6a2 | B. | (2x-1)•3x2y=6x3y-1 | ||
| C. | (-ab)3÷(-ab)=a2b2 | D. | ($\frac{1}{3}$)0×3=0 |
 已知二次函数y=ax2+bx+c的图象如图所示,试确定a,b,c,2a+b,2a-b,a+b+c,a-b+c的符号.
已知二次函数y=ax2+bx+c的图象如图所示,试确定a,b,c,2a+b,2a-b,a+b+c,a-b+c的符号.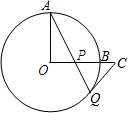 如图,已知⊙O的半径OA⊥OB,过点A的直线交OB于点P,交⊙O于点Q,过Q点引⊙O的切线交OB的延长线于点C,求证:CP=CQ.
如图,已知⊙O的半径OA⊥OB,过点A的直线交OB于点P,交⊙O于点Q,过Q点引⊙O的切线交OB的延长线于点C,求证:CP=CQ.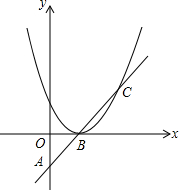 如图,抛物线y=ax2沿着x轴移动,与直线AB相交于B,C两点,若B(1,0)且OA=OB,AB=BC.
如图,抛物线y=ax2沿着x轴移动,与直线AB相交于B,C两点,若B(1,0)且OA=OB,AB=BC.