题目内容
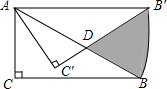 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是考点:旋转的性质,扇形面积的计算
专题:计算题
分析:根据含30度的直角三角形三边的关系得到AB=2AC=2,BC=
AC=
,根据互余得到∠CAB=60°,再根据旋转的性质得到AC′=AC=1,AB′=AB=2,B′C′=BC=
,∠B′AB=30°,∠C′AB′=∠CAB=60°,则∠C′AD=∠C′AB′∠BAB′=30°,接着在Rt△AC′D中,利用∠C′AD=30°可得C′D=
AC′=
,所以B′D=B′C′-C′D=
,然后根据三角形面积公式、扇形面积公式和图中阴影部分的面积=S扇形BAB′-S△ADB′进行计算即可.
| 3 |
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
解答:解:∵∠C=90°,∠ABC=30°,
∴∠CAB=60°,AB=2AC=2,
BC=
AC=
,
∵Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,
∴AC′=AC=1,AB′=AB=2,B′C′=BC=
,∠B′AB=30°,∠C′AB′=∠CAB=60°,
∴∠C′AD=∠C′AB′∠BAB′=30°,
在Rt△AC′D中,∵∠C′AD=30°,
∴C′D=
AC′=
,
∴B′D=B′C′-C′D=
-
=
,
∴图中阴影部分的面积=S扇形BAB′-S△ADB′
=
-
×
×1
=
.
故答案为
.
∴∠CAB=60°,AB=2AC=2,
BC=
| 3 |
| 3 |
∵Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,
∴AC′=AC=1,AB′=AB=2,B′C′=BC=
| 3 |
∴∠C′AD=∠C′AB′∠BAB′=30°,
在Rt△AC′D中,∵∠C′AD=30°,
∴C′D=
| ||
| 3 |
| ||
| 3 |
∴B′D=B′C′-C′D=
| 3 |
| ||
| 3 |
2
| ||
| 3 |
∴图中阴影部分的面积=S扇形BAB′-S△ADB′
=
| 30•π•22 |
| 360 |
| 1 |
| 2 |
2
| ||
| 3 |
=
π-
| ||
| 3 |
故答案为
π-
| ||
| 3 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了扇形面积的计算和含30度的直角三角形三边的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知OD平分∠AOB,OE平分∠BOD,若
如图,已知OD平分∠AOB,OE平分∠BOD,若| ∠AOC |
| ∠BOC |
| 3 |
| 2 |
| ∠COE |
| ∠BOE |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF.不能添加的一组条件是( )
如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF.不能添加的一组条件是( )| A、∠B=∠E,BC=EF |
| B、∠A=∠D,BC=EF |
| C、∠A=∠D,∠B=∠E |
| D、BC=EF,AC=DF |
下列结论错误的是( )
| A、0既不是正数,也不是负数 |
| B、两点之间线段最短 |
| C、锐角和钝角互补 |
| D、两点确定一条直线 |
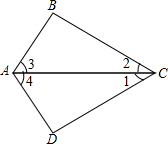 如图,AC是△ABC和△ADC的公共边,要判定△ABC≌△ADC还需要补充的条件不能是( )
如图,AC是△ABC和△ADC的公共边,要判定△ABC≌△ADC还需要补充的条件不能是( )| A、AB=AD,∠1=∠2 |
| B、AB=AD,∠3=∠4 |
| C、∠1=∠2,∠3=∠4 |
| D、∠1=∠2,∠B=∠D |
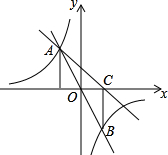 如图,在平面直角坐标系xOy中,直线y=mx与双曲线y=
如图,在平面直角坐标系xOy中,直线y=mx与双曲线y=