题目内容
 如图,一次函数y=ax+b(a≠0)与反比例函数y=
如图,一次函数y=ax+b(a≠0)与反比例函数y=| k |
| x |
(1)试确定一次函数与反比例函数的表达式.
(2)结合图象,直接写出不等式ax+b≥
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把A(-1,4)代入y=
(k≠0)求出k,从而得到反比例函数解析式为y=-
,再利用反比例函数解析式确定B点坐标,然后利用待定系数法求一次函数解析式;
(2)根据交点坐标,观察函数图象即可求得.
| k |
| x |
| 4 |
| x |
(2)根据交点坐标,观察函数图象即可求得.
解答:解:(1)把A(-1,4)代入y=
(k≠0)得k=-1×4=-4,
所以反比例函数解析式为y=-
,
把B(m,-2)代入y=-
得-2=-
,解得m=2,
所以B点坐标为(2,-2),
把A(-1,4)、B(2,-2)代入y=ax+b得
,解得
,
所以一次函数解析式为y=-2x+2;
(2)x≤-1或0<x≤2.
| k |
| x |
所以反比例函数解析式为y=-
| 4 |
| x |
把B(m,-2)代入y=-
| 4 |
| x |
| 4 |
| m |
所以B点坐标为(2,-2),
把A(-1,4)、B(2,-2)代入y=ax+b得
|
|
所以一次函数解析式为y=-2x+2;
(2)x≤-1或0<x≤2.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.

练习册系列答案
相关题目
 如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=1,DB=2,则△ADE的面积与△ABC的面积的比等于( )
如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=1,DB=2,则△ADE的面积与△ABC的面积的比等于( )A、
| ||
B、
| ||
C、
| ||
| D、1:9 |
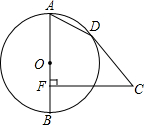 如图,AB是⊙O的直径,CD切⊙O于D,CF⊥AB于F,若tan∠A=2,求sin∠DCF的值.
如图,AB是⊙O的直径,CD切⊙O于D,CF⊥AB于F,若tan∠A=2,求sin∠DCF的值.
 如图,AB是⊙O的直径,CD切⊙O于C,OD⊥AB交AC于E,tan∠DEC=3,求sin∠D的值.
如图,AB是⊙O的直径,CD切⊙O于C,OD⊥AB交AC于E,tan∠DEC=3,求sin∠D的值.