题目内容
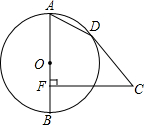 如图,AB是⊙O的直径,CD切⊙O于D,CF⊥AB于F,若tan∠A=2,求sin∠DCF的值.
如图,AB是⊙O的直径,CD切⊙O于D,CF⊥AB于F,若tan∠A=2,求sin∠DCF的值.考点:切线的性质
专题:
分析:连接DO并延长交CF的延长线于E,过D作DG⊥AB于G,根据切线的性质求得ED⊥DC,进而求得∠AOD=∠DCF,根据已知设AG=x,则GD=2x,设OA=OD=y,则OG=(y-x),在RT△OGD中,根据勾股定理得:OG2+GD2=OD2,即(y-x)2+(2x)2=y2,解得y=
x,解直角三角函数即可求得sin∠DCF的值.
| 5 |
| 2 |
解答: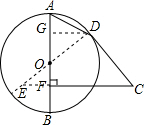 解:连接DO并延长交CF的延长线于E,过D作DG⊥AB于G,
解:连接DO并延长交CF的延长线于E,过D作DG⊥AB于G,
∵CD切⊙O于D,
∴ED⊥DC,
∵CF⊥AB,
∴∠EFO=∠EDC=90°,
∴∠EOF=∠DCF,
∵∠AOD=∠EOF,
∴∠AOD=∠DCF,
∵tan∠A=2,
∴
=2,
∴GD=2AG,
设AG=x,则GD=2x,
设OA=OD=y,则OG=(y-x),
在RT△OGD中,根据勾股定理得:OG2+GD2=OD2,
即(y-x)2+(2x)2=y2,解得y=
x,
∴sin∠DCF=sin∠GOD=
=
=
.
 解:连接DO并延长交CF的延长线于E,过D作DG⊥AB于G,
解:连接DO并延长交CF的延长线于E,过D作DG⊥AB于G,∵CD切⊙O于D,
∴ED⊥DC,
∵CF⊥AB,
∴∠EFO=∠EDC=90°,
∴∠EOF=∠DCF,
∵∠AOD=∠EOF,
∴∠AOD=∠DCF,
∵tan∠A=2,
∴
| GD |
| AG |
∴GD=2AG,
设AG=x,则GD=2x,
设OA=OD=y,则OG=(y-x),
在RT△OGD中,根据勾股定理得:OG2+GD2=OD2,
即(y-x)2+(2x)2=y2,解得y=
| 5 |
| 2 |
∴sin∠DCF=sin∠GOD=
| GD |
| OD |
| 2x | ||
|
| 4 |
| 5 |
点评:本题考查了切线的性质,勾股定理的应用,解直角三角函数,作出辅助线构建直角三角形是解题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
计算1-(-1)的结果是( )
| A、2 | B、1 | C、0 | D、-2 |
 如图,已知正△ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG=x,设△EFG的面积为y,则y关于x的函数关系式为( )
如图,已知正△ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG=x,设△EFG的面积为y,则y关于x的函数关系式为( )A、-
| ||||||||
B、-
| ||||||||
C、
| ||||||||
D、
|

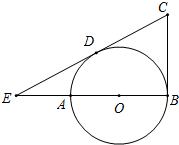 如图,AB是⊙O的直径,BC切⊙O于B,CD切⊙O于D,交AB的延长线于E.若BC=6,EB=8,求EA.
如图,AB是⊙O的直径,BC切⊙O于B,CD切⊙O于D,交AB的延长线于E.若BC=6,EB=8,求EA. 如图,一次函数y=ax+b(a≠0)与反比例函数y=
如图,一次函数y=ax+b(a≠0)与反比例函数y=