题目内容
已知等边△ABC中,点D为射线BA上一点,作DE=DC,交直线BC于点E.
(1)当点D在线段AB上时,如图1,线段CE、AD、AC之间的数量关系是 ;
(2)当点D在BA的延长线上时,如图2,求证:CE=AC-AD;
(3)在(2)的条件下,∠ABC的平分线BF,交CD于点F,过点A作AH⊥CD于H,当∠EDC=30°,CF=10,求DH的长.

(1)当点D在线段AB上时,如图1,线段CE、AD、AC之间的数量关系是
(2)当点D在BA的延长线上时,如图2,求证:CE=AC-AD;
(3)在(2)的条件下,∠ABC的平分线BF,交CD于点F,过点A作AH⊥CD于H,当∠EDC=30°,CF=10,求DH的长.

考点:全等三角形的判定与性质
专题:
分析:(1)作DF∥BC交AC于F,证出DF=AD,证明△DFC≌△EBD,得出DF=BE,得出BE=AD,BE+BC=AD+AC,CE=AD+AC;
(2)过D作DF∥AC交BC延长线于F,证明△BDE≌△CDF,得BE=CF,∴BE=AD,∴CE=BC-BE=AC-AD;
(3)连接AF,证明△ABF≌△CBF,得AF=CF,再证明DH=AH=
CF=5;
(2)过D作DF∥AC交BC延长线于F,证明△BDE≌△CDF,得BE=CF,∴BE=AD,∴CE=BC-BE=AC-AD;
(3)连接AF,证明△ABF≌△CBF,得AF=CF,再证明DH=AH=
| 1 |
| 2 |
解答:解:(1)作DF∥BC交AC于F,如图1所示:
∵△ABC是等边三角形,
∴AC=BC,∠ABC=∠BAC=∠ACB=60°,
∴∠DBE=120°,
∵DF∥BC,
∴∠ADF=∠ABC=60°,
∠AFD=∠ACB=60°,∠FDC=∠DCE,
∴∠A=∠ADF=∠AFD,∠DFC=120°,
∴△ADF是等边三角形,∠DFC=∠DBE,
∴DF=AD,
∵DE=DC,
∴∠E=∠DCE,
∴∠FDC=∠E,
在△DFC和△EBD中,
∴△DFC≌△EBD(AAS),
∴DF=BE,∴BE=AD,
∴BE+BC=AD+AC,CE=AD+AC;
(2)过D作DF∥AC交BC延长线于F,如图2所示:
则∠BDF=∠,BAC=60°,∠F=ACB=60°,
∴∠BDF=∠F=∠ABC,
∴BD=BF,∴AD=CF,
∵DE=DC,∴∠DEC=∠DCE,
∴∠DBE=∠DCF,
在△BDE和△CDF中,
∴△BDE≌△CDF(AAS),
∴BE=CF,
∴BE=AD,
∴CE=BC-BE=AC-AD;
(3)连接AF,如图3所示:
∵DE=DC,∠EDC=30°,
∴∠DEC=∠DCE=75°,
∴∠ACF=75°-60°=15°,
∵BF平分∠ABC,
∴∠ABF=∠CBF,
在△ABF和△CBF中,
,
△ABF≌△CBF(SAS),
∴AF=CF,
∴∠FAC=∠ACF=15°,
∴∠AFH=15°+15°=30°,
∵AH⊥CD,
∴AH=
AF=
CF=5,
∵∠DEC=∠ABC+∠BDE,
∴∠BDE=75°-60°=15°,
∴∠ADH=15°+30°=45°,
∴∠DAH=∠ADH=45°,
∴DH=AH=5.

∵△ABC是等边三角形,
∴AC=BC,∠ABC=∠BAC=∠ACB=60°,
∴∠DBE=120°,
∵DF∥BC,
∴∠ADF=∠ABC=60°,
∠AFD=∠ACB=60°,∠FDC=∠DCE,
∴∠A=∠ADF=∠AFD,∠DFC=120°,
∴△ADF是等边三角形,∠DFC=∠DBE,
∴DF=AD,
∵DE=DC,
∴∠E=∠DCE,
∴∠FDC=∠E,
在△DFC和△EBD中,
|
∴△DFC≌△EBD(AAS),
∴DF=BE,∴BE=AD,
∴BE+BC=AD+AC,CE=AD+AC;
(2)过D作DF∥AC交BC延长线于F,如图2所示:

则∠BDF=∠,BAC=60°,∠F=ACB=60°,
∴∠BDF=∠F=∠ABC,
∴BD=BF,∴AD=CF,
∵DE=DC,∴∠DEC=∠DCE,
∴∠DBE=∠DCF,
在△BDE和△CDF中,
|
∴△BDE≌△CDF(AAS),
∴BE=CF,
∴BE=AD,
∴CE=BC-BE=AC-AD;
(3)连接AF,如图3所示:

∵DE=DC,∠EDC=30°,
∴∠DEC=∠DCE=75°,
∴∠ACF=75°-60°=15°,
∵BF平分∠ABC,
∴∠ABF=∠CBF,
在△ABF和△CBF中,
|
△ABF≌△CBF(SAS),
∴AF=CF,
∴∠FAC=∠ACF=15°,
∴∠AFH=15°+15°=30°,
∵AH⊥CD,
∴AH=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠DEC=∠ABC+∠BDE,
∴∠BDE=75°-60°=15°,
∴∠ADH=15°+30°=45°,
∴∠DAH=∠ADH=45°,
∴DH=AH=5.
点评:本题考查了全等三角形的判定与性质;证明三角形全等是解决问题的关键,注意辅助线的作法.

练习册系列答案
相关题目
 如图,PA⊥OA于点A,PB⊥OB于点B,你认为再添加下列哪个条件也不能推出OP垂直平分AB( )
如图,PA⊥OA于点A,PB⊥OB于点B,你认为再添加下列哪个条件也不能推出OP垂直平分AB( )| A、OP⊥AB |
| B、OP平分∠AOB |
| C、PA=PB |
| D、∠OPA=∠OPB |
 如图,一次函数y=ax+b(a≠0)与反比例函数y=
如图,一次函数y=ax+b(a≠0)与反比例函数y= 若二次函数y=-x2+bx+c的部分图象如图所示,则关于x的一元二次方程-x2+bx+c=0的一个解是x1=3,则另一个解为
若二次函数y=-x2+bx+c的部分图象如图所示,则关于x的一元二次方程-x2+bx+c=0的一个解是x1=3,则另一个解为 如图,A、B两点在函数y=
如图,A、B两点在函数y=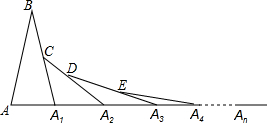 如图,在第1个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…按此作法进行下去,第n个三角形的以An为顶点的内角的度数为
如图,在第1个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…按此作法进行下去,第n个三角形的以An为顶点的内角的度数为 在Rt△ABC中,∠C=90°,若AB=4,sinA=
在Rt△ABC中,∠C=90°,若AB=4,sinA=