题目内容
1. 已知函数y=2+$\frac{4}{x}$.
已知函数y=2+$\frac{4}{x}$.(1)写出自变量x的取值范围:x≠0;
(2)请通过列表,描点,连线画出这个函数的图象:
①列表:
| x | … | -8 | -4 | -3 | -2 | -1 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | 8 | … |
| y | … | $\frac{3}{2}$ | 1 | $\frac{2}{3}$ | 0 | -2 | -6 | 10 | 6 | 4 | $\frac{10}{3}$ | 3 | $\frac{5}{2}$ | … |
③连线(将图中描出的各点用平滑的曲线连接起来,得到函数的图象).
(3)观察函数的图象,回答下列问题:
①图象与x轴有1个交点,所以对应的方程2+$\frac{4}{x}$=0实数根是x=-2;
②函数图象的对称性是A.
A、既是轴对称图形,又是中心对称图形
B、只是轴对称图形,不是中心对称图形
C、不是轴对称图形,而是中心对称图形
D、既不是轴对称图形也不是中心对称图形
(4)写出函数y=2+$\frac{4}{x}$与y=$\frac{4}{x}$的图象之间有什么关系?(从形状和位置方面说明)
分析 (1)根据分式有意义的条件即可得到结论;
(2)根据题意作出图象即可;
(3)①②根据图象即可得到结论;
(4)根据函数关系式即可得到结论.
解答  解:(1)自变量x的取值范围:x≠0;
解:(1)自变量x的取值范围:x≠0;
故答案为:x≠0;
(2)(2,4),(4,3)需要补上,如图所示;
(3)①图象与x轴有1个交点,所以对应的方程2+$\frac{4}{x}$=0实数根是x=-2,
②A,
故答案为:1,x=-2;A;
(4)将函数y=$\frac{4}{x}$的图象向上平移2个单位就可以得到函数y=2+$\frac{4}{x}$的图象.
点评 本题考查了反比例函数的性质,反比例函数的图象,正确的作出图象是解题的关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
12.列方程解应用题:为了保护环境,节约用水,深圳按照《关于调整市水务(集团)有限公司自来水价格的通知》(深发改{2011}459 号)规定对供水范围内的居民用水实行三级阶梯水价收费如下表:
(1)若小明家去年1月份用水量20立方米,他家应缴费46元.
(2)若小明家去年2月份用水量26立方米,缴费64.4元,请求出用水在22-30立方米之间收费标准a元/立方米?
(3)在(2)的条件下,若小明家去年8月份用水量增大,共缴费87.4元,请求出他家8月份的用水量多少立方米?
| 每户每月用水量 | 水费价格(单位:元/吨) |
| 不超过20 | 2.3 |
| 超过20吨且不超过30吨的部分 | a |
| 超过30吨的部分 | 4.6 |
(2)若小明家去年2月份用水量26立方米,缴费64.4元,请求出用水在22-30立方米之间收费标准a元/立方米?
(3)在(2)的条件下,若小明家去年8月份用水量增大,共缴费87.4元,请求出他家8月份的用水量多少立方米?
6. 甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示,则乙比甲每小时快( )
甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示,则乙比甲每小时快( )
 甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示,则乙比甲每小时快( )
甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示,则乙比甲每小时快( )| A. | 20km/h | B. | 30km/h | C. | 40km/h | D. | 50km/h |
11.在下列图形中,一定是中心对称图形,但不一定是轴对称图形的为( )
| A. | 正五边形 | B. | 正六边形 | C. | 等腰梯形 | D. | 平行四边形 |
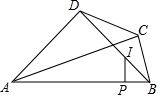 如图,Rt△ABC中,∠ACB=90°,CD为△ABC的外角平分线且∠ADB=90°.
如图,Rt△ABC中,∠ACB=90°,CD为△ABC的外角平分线且∠ADB=90°.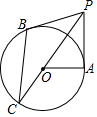 如图,PA、PB分别与⊙O相切于点A、B,PO的延长线交⊙O于点C,连接BC,OA.
如图,PA、PB分别与⊙O相切于点A、B,PO的延长线交⊙O于点C,连接BC,OA.