题目内容
16.近段时间共享单车风靡全国,从而刺激了自行车生产厂家,某厂家准备投入60万元生产A、B两种型号的共享单车.如果这60万元全部生产A型单车的数量比全部生产B型单车的数量少300辆,已知一辆A型单车的成本比一辆B型单车的成本多100元.(1)求生产一辆A型单车和生产一辆B型单车的成本各为多少元?
(2)由于共享单车公司需求量加大,生产厂家必须再生产A、B两种型号的单车共10000辆,恰逢原料商对基本原料的价格进行调整.调整后,A型单车每辆成本价比原来降低10%,B型单车每辆的成本价比原来增加20%,如果厂家准备投人的总成本不超过471万元,那么至少要生产多少辆A型单车?
(3)在(2)的条件下,该生产厂家发现,销售过程中每辆A型单车可获利150元,每辆B型单车可获利180元,厂家如何设计生产方案才能获得最大利润?最大利润是多少?
分析 (1)设生产一辆B型单车的成本为x元,则生产一辆A型单车的成本为(x+100)元,根据数量=总价÷单价结合60万元全部生产A型单车的数量比全部生产B型单车的数量少300辆,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设生产A型单车m辆,则生产B型单车(10000-m)辆,根据总成本=单辆成本×生产数量结合总成本不超过471万元,即可得出关于m的一元一次不等式,解之即可得出结论;
(3)设该厂获得的总利润为y元,根据总利润=单辆利润×生产辆数,即可得出y关于m的函数关系式,根据一次函数的性质结合m的取值范围,即可解决最值问题.
解答 解:(1)设生产一辆B型单车的成本为x元,则生产一辆A型单车的成本为(x+100)元,
根据题意得:$\frac{600000}{x}$-$\frac{600000}{x+100}$=300,
解得:x=400或x=-500(不合题意,舍去),
经检验,x=400是原分式方程的解,
∴x+100=500.
答:生产一辆B型单车的成本为400元,生产一辆A型单车的成本为500元.
(2)设生产A型单车m辆,则生产B型单车(10000-m)辆,
根据题意得:500×(1-10%)m+400×(1+20%)(10000-m)≤4710000,
解得:m≥3000.
答:至少要生产3000辆A型单车.
(3)设该厂获得的总利润为y元,
根据题意得:y=150m+180(10000-m)=1800000-30m,
∵-30<0,
∴y值随m的增大而减小,
∴当m=3000时,y取最大值,此时y=1800000-30×3000=1710000.
答:生产3000辆A型单车、7000辆B型单车时,获得的利润最大,最大值为171万元.
点评 本题考查了一次函数的应用、分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)根据数量=总价÷单价列出关于x的分式方程:(2)根据总成本=单辆成本×生产数量结合总成本不超过471万元,列出关于m的一元一次不等式;(3)根据总利润=单辆利润×生产辆数,找出y关于m的函数关系式.

| A. | -$\frac{12}{7}$≤t<-$\frac{8}{7}$ | B. | -$\frac{12}{7}$≤t<-$\frac{3}{2}$ | C. | -$\frac{3}{2}$≤t<-$\frac{4}{3}$ | D. | -$\frac{4}{3}$≤t<-$\frac{8}{7}$ |
 已知函数y=2+$\frac{4}{x}$.
已知函数y=2+$\frac{4}{x}$.(1)写出自变量x的取值范围:x≠0;
(2)请通过列表,描点,连线画出这个函数的图象:
①列表:
| x | … | -8 | -4 | -3 | -2 | -1 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | 8 | … |
| y | … | $\frac{3}{2}$ | 1 | $\frac{2}{3}$ | 0 | -2 | -6 | 10 | 6 | 4 | $\frac{10}{3}$ | 3 | $\frac{5}{2}$ | … |
③连线(将图中描出的各点用平滑的曲线连接起来,得到函数的图象).
(3)观察函数的图象,回答下列问题:
①图象与x轴有1个交点,所以对应的方程2+$\frac{4}{x}$=0实数根是x=-2;
②函数图象的对称性是A.
A、既是轴对称图形,又是中心对称图形
B、只是轴对称图形,不是中心对称图形
C、不是轴对称图形,而是中心对称图形
D、既不是轴对称图形也不是中心对称图形
(4)写出函数y=2+$\frac{4}{x}$与y=$\frac{4}{x}$的图象之间有什么关系?(从形状和位置方面说明)
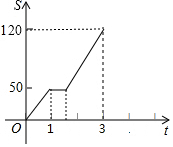 小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )
小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )| A. | 0.5小时 | B. | 0.6小时 | C. | 0.7小时 | D. | 0.8小时 |
| A. | a<0 | B. | a=0 | C. | a>0 | D. | a≥0 |

 如图中的四边形均为矩形,根据图形,利用图中的字母,写出一个正确的等式:(m+n)(a+b)=ma+mb+na+nb(答案不唯一).
如图中的四边形均为矩形,根据图形,利用图中的字母,写出一个正确的等式:(m+n)(a+b)=ma+mb+na+nb(答案不唯一).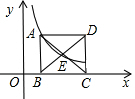 已知点(1,3)在函数y=$\frac{k}{x}$(x>0)的图象上,正方形ABCD的边BC在x轴上,点E是对角线AC、BD的交点,函数y=$\frac{k}{x}$(x>0)的图象又经过A、E两点,则点E的坐标为($\sqrt{6}$,$\frac{\sqrt{6}}{2}$).
已知点(1,3)在函数y=$\frac{k}{x}$(x>0)的图象上,正方形ABCD的边BC在x轴上,点E是对角线AC、BD的交点,函数y=$\frac{k}{x}$(x>0)的图象又经过A、E两点,则点E的坐标为($\sqrt{6}$,$\frac{\sqrt{6}}{2}$).