题目内容
7.在△ABC中,∠C=90°,BC:AC=1:$\sqrt{3}$,CD⊥AB于D,求△ABC与△CDB的面积之比?分析 BC=a则AC=$\sqrt{3}$a,由勾股定理可得AB=2a,证△ABC∽△CBD,根据相似三角形性质得$\frac{{S}_{△ABC}}{{S}_{△CBD}}$=$(\frac{AB}{CB})^{2}$即可.
解答 解:如图,设BC=a,则AC=$\sqrt{3}$a,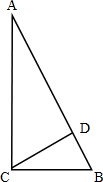
∵∠ACB=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=2a,
∵CD⊥AB,
∴∠CDB=∠ACB=90°,
又∵∠B=∠B,
∴△ABC∽△CBD,
∴$\frac{{S}_{△ABC}}{{S}_{△CBD}}$=$(\frac{AB}{CB})^{2}$=$(\frac{2a}{a})^{2}$=4,
故△ABC与△CDB的面积之比为4:1.
点评 本题主要考查相似三角形的判定与性质,由勾股定理得AB长是前提,证三角形相似得面积比等于相似比是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图:AB为的⊙0弦;点D和C在⊙0上;且有AD=BC,求证:△ABD≌△BAC.
如图:AB为的⊙0弦;点D和C在⊙0上;且有AD=BC,求证:△ABD≌△BAC. 已知关于x的一元二次方程mx2+(3m+1)x+3=0.
已知关于x的一元二次方程mx2+(3m+1)x+3=0.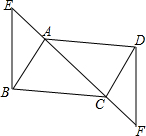 已知如图,E、F为?ABCD的对角线AC所在直线上的两点,AE=CF,求证:BE=DF.(用两种方法证明)
已知如图,E、F为?ABCD的对角线AC所在直线上的两点,AE=CF,求证:BE=DF.(用两种方法证明)