题目内容
9.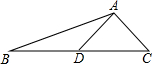 如图,AD是△ABC的中线,tanB=$\frac{1}{3}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.求:
如图,AD是△ABC的中线,tanB=$\frac{1}{3}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.求:(1)BC的长;
(2)尺规作图(保留作图痕迹,不写作法):作出△ABC的外接圆,并求外接圆半径.
分析 (1)过点A作AE⊥BC于点E,根据三角函数的定义和特殊角的三角函数即可得出答案;
(2)作AB、AC的垂直平分线,交点O即为圆心,以OA为半径作圆,即可得出△ABC的外接圆,根据sin∠ABC=sin∠AOK即可解决问题.
解答  解:(1)过点A作AE⊥BC于点E,
解:(1)过点A作AE⊥BC于点E,
∵cosC=$\frac{\sqrt{2}}{2}$,
∴∠C=45°,
在Rt△ACE中,CE=AC•cosC=1,
∴AE=CE=1,
在Rt△ABE中,tanB=$\frac{1}{3}$,即$\frac{AE}{BE}$=$\frac{1}{3}$,
∴BE=3AE=3,
∴BC=BE+CE=4;
(2)如图,①作线段AB的垂直平分线NM.
②作线段AC的垂直平分线GH与直线MN的交点O就是△ABC外接圆的圆心.
③以点O为圆心OA为半径作圆.
⊙O就是所求作的△ABC的外接圆.
∵∠AOC=2∠ABC,∠AOK=∠COK,
∴∠ABC=∠AOK,
∵sin∠AOK=sin∠ABC=$\frac{AE}{AB}$=$\frac{AK}{AO}$,
由(1)可知AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=$\sqrt{10}$,
∴$\frac{1}{\sqrt{10}}$=$\frac{\frac{\sqrt{2}}{2}}{AO}$,
∴AO=$\sqrt{5}$.
点评 本题考查的是解直角三角形的知识,正确作出辅助线构造直角三角形是解题的关键,注意锐角三角函数的概念的正确应用,本题也可以用相似三角形求半径,属于中考常考题型.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
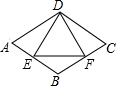 如图所示,菱形ABCD的周长为16cm,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为E,F,则△DEF的周长为6$\sqrt{3}$cm.
如图所示,菱形ABCD的周长为16cm,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为E,F,则△DEF的周长为6$\sqrt{3}$cm.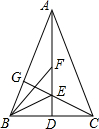 如图,△ABC中,AB=AC,AD⊥BC于点D,射线BE、BF将∠ABC三等分交AD于E、F两点,连接CE并延长交AB于点G,求证:$\frac{AF}{EF}$=$\frac{AG}{GB}$.
如图,△ABC中,AB=AC,AD⊥BC于点D,射线BE、BF将∠ABC三等分交AD于E、F两点,连接CE并延长交AB于点G,求证:$\frac{AF}{EF}$=$\frac{AG}{GB}$.
 如图,已知∠BAC=∠ACD,则可判断图中AB∥CD.
如图,已知∠BAC=∠ACD,则可判断图中AB∥CD.