题目内容
4.如图,在坐标系中,A(0,6),B(-2,0),C(3,0),∠BAC=45°,BD⊥AC,M(4,0),动点P从点M出发,沿x轴正方向,以每秒2个单位长度运动t秒(1)求D点坐标;
(2)连接PD、PE,设△PDE的面积为S,用t的代数式表示S
(3)点F为直线AC上一点,点P的运动过程中,是否存在这样的点P,使△PCF与△AED全等?若存在,求出t值;若不存在,说明理由.
分析 (1)先利用面积法求出AD=BD=2$\sqrt{5}$,再由DN∥AO得$\frac{DN}{AO}=\frac{CN}{CO}=\frac{CD}{CA}$,得CN=1,DN=2,由此即可解决问题.
(2)根据s=S△PDE-S△PEB即可解决问题.
(3)分两种情形讨论:①如图当△P1F1C≌△ADE,②当△F2P2C≌△ADE分别求出PC即可解决问题.
解答 解:(1)作DN⊥OC于N,
在RT△AOC中,AC=$\sqrt{A{O}^{2}+O{C}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,
∵∠BAD=45°,∠ADB=90°,
∴∠BAD=∠ABD=45°,
∴AD=BD
∵$\frac{1}{2}$•BC•OA=$\frac{1}{2}$•AC•BD,
∴BD=$\frac{BC•AO}{AC}$=2$\sqrt{5}$,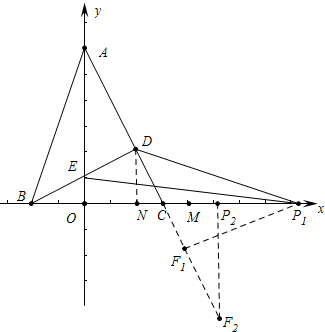
∵DN∥AO,
∴$\frac{DN}{AO}=\frac{CN}{CO}=\frac{CD}{CA}$,
∴CN=1,DN=2,
∴点D坐标(2,2),
(2)∵EO∥DN,BO=ON,
∴BE=ED,OE=$\frac{1}{2}$DN=1,
s=S△PDE-S△PEB=$\frac{1}{2}$•(6+2t)•2-$\frac{1}{2}$•(6+2t)•1=t+3.
(3)①如图当△P1F1C≌△ADE时,P1C=AE=5,
∴P1M=4,t=2.
②当△F2P2C≌△ADE时,P2C=ED=$\sqrt{5}$,
∴P2M=$\sqrt{5}$-1,
∴t=$\frac{\sqrt{5}-1}{2}$.
综上所述t=2或$\frac{\sqrt{5}-1}{2}$时,△PCF与△AED全等.
点评 本题考查坐标与图形的性质、勾股定理、全等三角形的性质、平行线分线段成比例定理等知识,解决问题的关键是利用面积法求出线段BD,学会分类讨论的思想,属于中考常考题型.

 如图,AB∥CD,那么( )
如图,AB∥CD,那么( )| A. | ∠1=∠4 | B. | ∠1=∠3 | C. | ∠2=∠3 | D. | ∠1=∠5 |
| A. | 四边相等的四边形是正方形 | |
| B. | 四角相等的四边形是正方形 | |
| C. | 对角线互相垂直的平行四边形是正方形 | |
| D. | 有一个角是直角的菱形是正方形 |
 如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF.
如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF.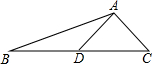 如图,AD是△ABC的中线,tanB=$\frac{1}{3}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.求:
如图,AD是△ABC的中线,tanB=$\frac{1}{3}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.求: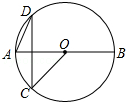 如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=65°,则∠OCD=40°.
如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=65°,则∠OCD=40°.