题目内容
16.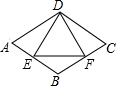 如图所示,菱形ABCD的周长为16cm,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为E,F,则△DEF的周长为6$\sqrt{3}$cm.
如图所示,菱形ABCD的周长为16cm,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为E,F,则△DEF的周长为6$\sqrt{3}$cm.
分析 首先作辅助线:连接BD,易得△ABD与△BCD是等边三角形,即可得△DEF是等边三角形,由勾股定理可求得△DEF的周长.
解答  解:连接AC,
解:连接AC,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=4cm,∠A=∠C=60°,
∴△ABD与△BCD是等边三角形,
∵DE⊥AB,DF⊥BC,
∴E、F分别为BC、CD的中点,
∴AE=AF=2cm,∠BDE=∠CAE=∠CDF=∠BDF=30°,
∴∠EDF=60°,即△DEF是等边三角形,
∴DE=DF=EF=2$\sqrt{3}$cm,
∴△DEF的周长为6$\sqrt{3}$cm.
故答案为:6$\sqrt{3}$cm.
点评 此题考查了菱形的性质:菱形的四条边都相等以及等边三角形的性质:三线合一,正确得出△DEF是等边三角形是解题关键.

练习册系列答案
相关题目
11. 如图,AB∥CD,那么( )
如图,AB∥CD,那么( )
 如图,AB∥CD,那么( )
如图,AB∥CD,那么( )| A. | ∠1=∠4 | B. | ∠1=∠3 | C. | ∠2=∠3 | D. | ∠1=∠5 |
 如图,在?ABCD中,∠DAB的角平分线交边CD于点E,AD=3,EC=2,则?ABCD的周长为16.
如图,在?ABCD中,∠DAB的角平分线交边CD于点E,AD=3,EC=2,则?ABCD的周长为16.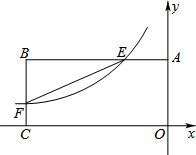 如图,反比例函数$y=\frac{k}{x}$(k<0)的图象与矩形OABC的边相交于E、F两点,连接EF,且BE=2AE,点E坐标为(-2,3).
如图,反比例函数$y=\frac{k}{x}$(k<0)的图象与矩形OABC的边相交于E、F两点,连接EF,且BE=2AE,点E坐标为(-2,3).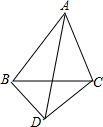 在△ABC中,AB=3,∠BAC=60°,把线段BC绕C点逆时针旋转得到线段CD,∠ACB+∠ACD=180°,AD=$\sqrt{19}$,则线段BC的长度为$\frac{\sqrt{31}}{2}$.
在△ABC中,AB=3,∠BAC=60°,把线段BC绕C点逆时针旋转得到线段CD,∠ACB+∠ACD=180°,AD=$\sqrt{19}$,则线段BC的长度为$\frac{\sqrt{31}}{2}$.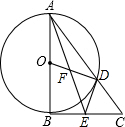 如图,在△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,E是BC的中点,连接AE、OD、DE、AE与OD相交于F.
如图,在△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,E是BC的中点,连接AE、OD、DE、AE与OD相交于F.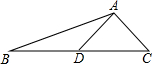 如图,AD是△ABC的中线,tanB=$\frac{1}{3}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.求:
如图,AD是△ABC的中线,tanB=$\frac{1}{3}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.求: