题目内容
1.如果线段b是线段a,c的比例中项,a:c=4:9,那么下列结论中正确的是( )| A. | a:b=4:9 | B. | b:c=2:3 | C. | a:b=3:2 | D. | b:c=3:2 |
分析 首先由a:c=4:9,根据比例的基本性质得出9a=4c,则a=$\frac{4}{9}$c,c=$\frac{9}{4}$a.再根据比例中项的概念,可得a:b=b:c,即b2=ac,那么b=$\frac{2}{3}$c=$\frac{3}{2}$a,进而求解即可.
解答 解:∵a:c=4:9,
∴9a=4c,
∴a=$\frac{4}{9}$c,c=$\frac{9}{4}$a.
∵线段b是线段a,c的比例中项,
∴a:b=b:c,即b2=ac=$\frac{4}{9}$c2=$\frac{9}{4}$a2,
∴b=$\frac{2}{3}$c=$\frac{3}{2}$a,
∴a:b=$\frac{4}{9}$c:$\frac{2}{3}$c=2:3,
∴b:c=a:b=2:3,
故选B.
点评 本题考查了比例线段,比例中项的概念,得出a=$\frac{4}{9}$c,b=$\frac{2}{3}$c是解题的关键.也考查了比例的基本性质.

练习册系列答案
相关题目
12.下列等式中是一元一次方程的是( )
| A. | 3x+2y=1 | B. | x2+1=2 | C. | m-3=6 | D. | $\frac{1}{x}$-5=-2 |
10.我国第六次人口普查显示,全国人口为1370000000人,用科学记数法表示数字1370000000为( )
| A. | 13.7×108 | B. | 1.37×109 | C. | 1.37×108 | D. | 0.137×1010 |
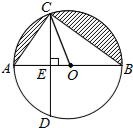 如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,OC=2.
如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,OC=2. 如图某超市举行“翻牌”抽奖活动,在一张木板上共有6个相同的牌,其分别对应价值为2元、5元、8元、10元、20元和50元的奖品.
如图某超市举行“翻牌”抽奖活动,在一张木板上共有6个相同的牌,其分别对应价值为2元、5元、8元、10元、20元和50元的奖品.