题目内容
13.已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-3),与x轴交于A、B两点,A(-1,0).求这条抛物线的表达式.分析 设抛物线的表达式为y=a(x-2)2-1(a≠0),将点C的坐标代入即可得出答案.
解答 解:∵抛物线的顶点C(1,-3),
∴可设该函数解析式为:y=a(x-1)2-3(a≠0),
又∵抛物线y=ax2+bx+c(a≠0)与与x轴交于A(-1,0),
∴0=a(-1-1)2-3,
解得a=$\frac{3}{4}$,
∴该抛物线的解析式是y=$\frac{3}{4}$(x-1)2-3.
点评 本题考查了待定系数法求二次函数的解析式,熟练掌握待定系数法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.如果线段b是线段a,c的比例中项,a:c=4:9,那么下列结论中正确的是( )
| A. | a:b=4:9 | B. | b:c=2:3 | C. | a:b=3:2 | D. | b:c=3:2 |
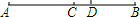
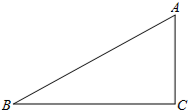 如图,在Rt△ABC中,∠C=90°,AC=3,tanB=$\frac{1}{2}$.
如图,在Rt△ABC中,∠C=90°,AC=3,tanB=$\frac{1}{2}$.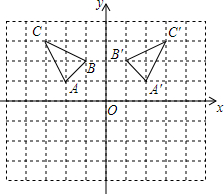 如图是一个8×10正方形格纸,△ABC中A点坐标为(-2,1).
如图是一个8×10正方形格纸,△ABC中A点坐标为(-2,1).