题目内容
16.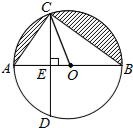 如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,OC=2.
如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,OC=2.(1)求OE和CD的长;
(2)求弧BD的长及图中阴影部分的面积.
分析 (1)在△OCE中,利用三角函数即可求得CE,OE的长,再根据垂径定理即可求得CD的长;
(2)根据弧长公式即可得到弧BD的长,根据半圆的面积减去△ABC的面积,即可得到阴影部分的面积.
解答 解:(1)在△OCE中,
∵∠CEO=90°,∠EOC=60°,OC=2,
∴OE=$\frac{1}{2}$OC=1,
∴CE=$\frac{\sqrt{3}}{2}$OC=$\sqrt{3}$,
∵OA⊥CD,
∴CE=DE,
∴CD=2$\sqrt{3}$;
(2)∵CD⊥AB,
∴$\widehat{BD}=\widehat{BC}$,
∵∠EOC=60°,
∴∠BOC=120°,
∴弧BD的长=$\frac{120•2π×2}{360}$=$\frac{4π}{3}$,
∵S△ABC=$\frac{1}{2}$AB•EC=$\frac{1}{2}$×4×$\sqrt{3}$=2$\sqrt{3}$,
∴S阴影=$\frac{1}{2}π×{2}^{2}-2\sqrt{3}$=2π-2$\sqrt{3}$.
点评 本题主要考查了垂径定理以及三角函数,弧长的计算,一些不规则的图形的面积可以转化为规则图形的面积的和或差求解.

练习册系列答案
相关题目
7.已知(a+3)2+|b-2|=0,则2ab的值是( )
| A. | -6 | B. | 18 | C. | -12 | D. | 9 |
11.已知P1(-3,y1),P2(-3,y2)是一次函数y=2x-b的图象上的两个点,则y1、y2的大小关系是( )
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 不能确定 |
1.如果线段b是线段a,c的比例中项,a:c=4:9,那么下列结论中正确的是( )
| A. | a:b=4:9 | B. | b:c=2:3 | C. | a:b=3:2 | D. | b:c=3:2 |
6.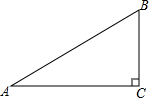 如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列不正确的是( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列不正确的是( )
 如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列不正确的是( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列不正确的是( )| A. | ∠B=60° | B. | a=5 | C. | b=5$\sqrt{3}$ | D. | tanB=$\frac{\sqrt{3}}{3}$ |
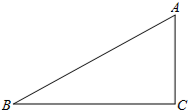 如图,在Rt△ABC中,∠C=90°,AC=3,tanB=$\frac{1}{2}$.
如图,在Rt△ABC中,∠C=90°,AC=3,tanB=$\frac{1}{2}$.