题目内容
11. 如图某超市举行“翻牌”抽奖活动,在一张木板上共有6个相同的牌,其分别对应价值为2元、5元、8元、10元、20元和50元的奖品.
如图某超市举行“翻牌”抽奖活动,在一张木板上共有6个相同的牌,其分别对应价值为2元、5元、8元、10元、20元和50元的奖品.(1)小雷在该抽奖活动中随机翻一张牌,求抽中10元奖品的概率;
(2)如果随机翻两张牌,且第一次翻过的牌不再参加下次翻牌,求两次抽中的奖品的总价值大于14元的概率.
分析 (1)随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数,据此用1除以6,即可得出结果.
(2)首先应用树状图法,列举出随机翻2张牌,所获奖品的总值一共有多少种情况;然后用两次抽中的奖品的总价值大于14元的情况的数量除以所有情况的数量即可.
解答 解:(1)共有6个可能的结果,抽中10元奖品的结果有1个,
∴抽中10元奖品的概率为$\frac{1}{6}$.
(2)画树状图:
共有30种可能的结果,两次抽中的奖品的总价值大于14元的结果有22个,
∴两次抽中的奖品的总价值大于14元的概率=$\frac{22}{30}$=$\frac{11}{15}$.
点评 (1)此题主要考查了概率公式,要熟练掌握,解答此题的关键是要明确:随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.
(2)此题还考查了列举法与树状图法求概率问题,解答此类问题的关键在于列举出所有可能的结果,列表法是一种,但当一个事件涉及三个或更多元素时,为不重不漏地列出所有可能的结果,通常采用树形图.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.如果线段b是线段a,c的比例中项,a:c=4:9,那么下列结论中正确的是( )
| A. | a:b=4:9 | B. | b:c=2:3 | C. | a:b=3:2 | D. | b:c=3:2 |
6.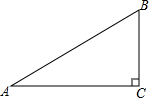 如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列不正确的是( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列不正确的是( )
 如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列不正确的是( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列不正确的是( )| A. | ∠B=60° | B. | a=5 | C. | b=5$\sqrt{3}$ | D. | tanB=$\frac{\sqrt{3}}{3}$ |
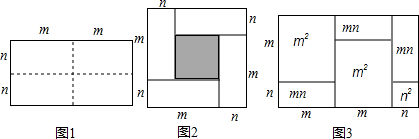
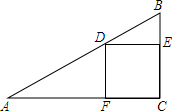 正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上.
正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上.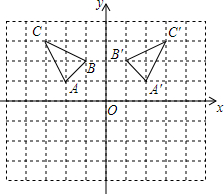 如图是一个8×10正方形格纸,△ABC中A点坐标为(-2,1).
如图是一个8×10正方形格纸,△ABC中A点坐标为(-2,1).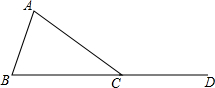 如图,点D在△ABC的BC边的延长线上,且∠A=∠B.
如图,点D在△ABC的BC边的延长线上,且∠A=∠B.