题目内容
7. 如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D.
如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D.(1)利用尺规作⊙O,使⊙O经过点A,D,且圆心O在AB上,并标出⊙O与AB的另一个交点E(保留作图痕迹,不写作法);
(2)在你所作的图中,
①判断直线BC与⊙O的位置关系,并说明理由;
②若AB=6cm,BD=2$\sqrt{3}$cm,求:线段BD,BE与劣弧$\widehat{DE}$所围成的图形面积(结果保留根号和π)
分析 (1)分别以A、D为圆心,以大于$\frac{1}{2}$AD为半径画弧,交于点M、N,作直线MN,交线段AB于点O,再以O为圆心,以OA或OD为半径画圆交AB于E,则⊙O就是所求作的圆;
(2)①连接OD,证AC∥OD得∠ODB=∠C=90°,则BC与⊙O相切;
②设⊙O半径为x,根据勾股定理求出圆O的半径,则所求图形面积=S△ODB-S扇形ODE,代入面积公式计算即可.
解答 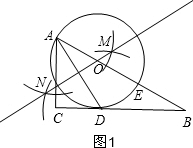 解:(1)如图1所示:
解:(1)如图1所示:
(2)①如图2,BC与⊙O相切,理由是:
连接OD,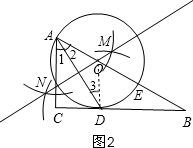
∵AD平分∠CAB,
∴∠1=∠2,
∵OA=OD,
∴∠2=∠3,
∴∠1=∠3,
∴AC∥OD,
∴∠ODB=∠C=90°,
∴BC与⊙O相切;
②如图2,设⊙O半径为x,则OA=OD=x,OB=6-x,
在Rt△ODB中,OD2+BD2=OB2,
∴x2+(2$\sqrt{3}$)2=(6-x)2,
x=2,
∴OD=2,OB=6-2=4,
∴∠B=30°,∠DOB=90°-30°=60°,
设线段BD,BE与劣弧$\widehat{DE}$所围成的图形面积为S,
则S=S△ODB-S扇形ODE=$\frac{1}{2}$×2×2$\sqrt{3}$-$\frac{60π×{2}^{2}}{360}$=2$\sqrt{3}$-$\frac{2π}{3}$;
∴线段BD,BE与劣弧$\widehat{DE}$所围成的图形面积为(2$\sqrt{3}$-$\frac{2π}{3}$)cm2.
点评 本题是圆的综合题,综合考查了尺规作圆、扇形面积公式、勾股定理和切线的证明,难度不大;过两点作圆,直接作两点为线段的垂直平分线,圆心就是这条垂直平分线上;在判定一条直线是否为圆的切线时,①当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径,可简单的说成“无交点,作垂线段,证半径”;②当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线,可简单地说成“有交点,作半径,证垂直”,本题就是第二种情况,有交点,作半径,证垂直.

 如图,表示下列某个不等式的解集,其中正确的是( )
如图,表示下列某个不等式的解集,其中正确的是( )| A. | x>2 | B. | x<2 | C. | x≥2 | D. | x≤-2 |
 如图所示,⊙O是△ABC 的外接圆,AB是直径,∠ABC=30°,点E是OC的中点,连接AE并延长交⊙○于点D,连接OD,CD,BD.
如图所示,⊙O是△ABC 的外接圆,AB是直径,∠ABC=30°,点E是OC的中点,连接AE并延长交⊙○于点D,连接OD,CD,BD.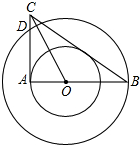 如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
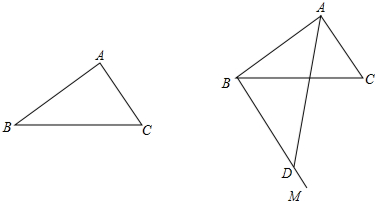
如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB. 如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O,求证:△ABC≌△DCB.
如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O,求证:△ABC≌△DCB.