题目内容
7.如图,AB∥CD,P为定点,E、F分别是AB、CD上的动点.(1)求证:∠P=∠BEP+∠PFD;
(2)若M为CD上一点,MN交PF于N.证明:∠PNM=∠NMF+∠NFM;(说明:不能运用三角形内角和定理)
(3)在(2)的基础上,若∠FMN=∠BEP,试说明∠EPF与∠PNM的关系,并证明你的结论.

分析 (1)过P作PQ平行于AB,由AB与CD平行,得到PQ与CD平行,利用两直线平行内错角相等得到两对角相等,再由∠EPF=∠1+∠2,等量代换就可得证;
(2)作NH∥DC,利用平行线的性质得出∠PNH=∠NFM,∠MNH=∠NMF,得出结论;
(3)由(1)(2)中的结论∠EPF=∠BEP+∠PFD,∠PNM=∠NMF+∠NFM;根据∠FMN=∠BEP,等量代换即可得证.
解答 解:(1)如图,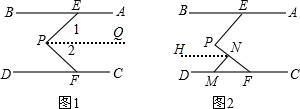
过P作PQ∥AB,
∵AB∥CD,
∴PQ∥CD,
∴∠BEP=∠1,∠2=∠PFD,
∵∠EPF=∠1+∠2,
∴∠EPF=∠BEP+∠PFD;
(2)∵作NH∥DC,
∴∠PNH=∠NFM,∠MNH=∠NMF,
∴∠PNM=∠PNH+∠MNH=∠NMF+∠NFM.
(3)由(1)的结论∠EPF=∠BEP+∠PFD,
∵∠FMN=∠BEP,
∴∠EPF=∠FMN+∠PFD,
∵∠PNM=∠NMF+∠NFM,
∴∠PMN=∠FMN+∠PFD,
则∠EPF=∠PMN.
点评 此题考查了平行线的性质,熟练掌握平行线的性质是解本题的关键.

练习册系列答案
相关题目
2.如果一元二次方程x2+12x+27=0的两个根是x1,x2,那么x1+x2的值为( )
| A. | -6 | B. | -12 | C. | 12 | D. | 27 |
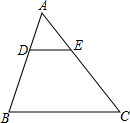 如图,在△ABC中,D、E分别是AB、AC上点,且AE=3,AD=2,DB=4,AB=9,△ADE与△ABC相似吗?为什么?
如图,在△ABC中,D、E分别是AB、AC上点,且AE=3,AD=2,DB=4,AB=9,△ADE与△ABC相似吗?为什么?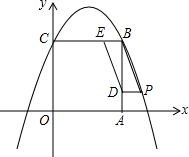 如图,在直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在x轴、y轴的正半轴上.抛物线y=-x2+bx+c经过点B、C.
如图,在直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在x轴、y轴的正半轴上.抛物线y=-x2+bx+c经过点B、C. 如图,⊙O是△ABC的外接圆,弦CD⊥AB,CE是直径,F是弧AB的中点,求证:
如图,⊙O是△ABC的外接圆,弦CD⊥AB,CE是直径,F是弧AB的中点,求证: 敌军基地在三条公路围成的三角区域内,我军一队战士在一条公路中点垂直射击,另一队战士在另一条公路中点垂直射击,均击中敌军基地,问第三队战士在公路何处垂直射击可击中目标?
敌军基地在三条公路围成的三角区域内,我军一队战士在一条公路中点垂直射击,另一队战士在另一条公路中点垂直射击,均击中敌军基地,问第三队战士在公路何处垂直射击可击中目标?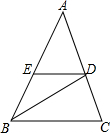 如图,在△ABC中,AB=AC,BD是∠ABC的平分线,DE∥BC,则CD=DE.请说明理由.
如图,在△ABC中,AB=AC,BD是∠ABC的平分线,DE∥BC,则CD=DE.请说明理由.
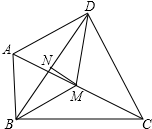 如图,在四边形ABCD中,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,求证:
如图,在四边形ABCD中,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,求证: