题目内容
16.如图,将不同的正多边形对折不同的次数都可以得到一个三角形,用剪刀在三角形上,随意剪去一条线,你就会得到不同的轴对称图案.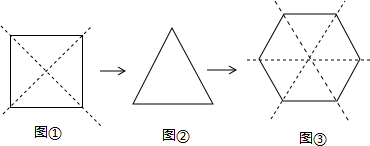
(1)将图①正方形纸片沿虚线对折2次,所得的图形至少有2条对称轴;
(2)将图③正六边形纸片沿虚线对折3次,所得的图形至少有3条对称轴;
(3)一张正八边形的纸片应对折几次才能得到一个三角形,所得的图形至少有几条对称轴?如果换成正十边形呢?
(4)你发现其中的规律了吗?请你把你的发现写出来.
分析 (1)可动手进行操作,得到图形进行展开,观察后可得答案;
(2)可动手进行操作,得到图形进行展开,观察后可得答案;
(3)可动手进行操作,得到图形进行展开,观察后可得答案;
(4)由以上可得规律,对折次数与对称轴条数的关系.
解答 解:(1)将图①正方形纸片沿虚线对折2次,所得的图形至少有2条对称轴;
故答案为:2;
(2)将图③正六边形纸片沿虚线对折3次,所得的图形至少有3条对称轴;
故答案为:3;
(3)一张正八边形的纸片应对折4次才能得到一个三角形,所得的图形至少有4条对称轴,
如果换成正十边形的纸片应对折5次才能得到一个三角形,所得的图形至少有5条对称轴;
(4)一张正n边形的纸片对折$\frac{n}{2}$次,可以得到一个三角形,
用剪刀在三角形上任意剪出一条线所得到的图形至少有$\frac{n}{2}$条对称轴.
点评 本题考查了翻折变换、轴对称图形及剪纸问题;动手操作是正确解答此类问题的很好的方法,做题时注意应用.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
6.下列各组条件中,能判定△ABC≌△DEF的是( )
| A. | AB=DE,BC=EF,∠A=∠D | B. | ∠A=∠D,∠C=∠F,AC=EF | ||
| C. | AB=DE,BC=EF,AC=DF | D. | ∠B=∠E |

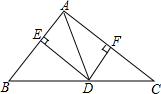 如图,在△ABC中,AB=3cm,AC=4cm,AD是BC的中线,DE,DF分别是△ABD和△ACD的高,求DE:DF的值.
如图,在△ABC中,AB=3cm,AC=4cm,AD是BC的中线,DE,DF分别是△ABD和△ACD的高,求DE:DF的值.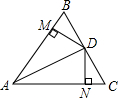 如图所示,△ABC中,AD平分∠BAC,点D是BC的中点,DM⊥AB,DN⊥AC,垂足分别为M,N,求证:∠B=∠C,BM=CN.
如图所示,△ABC中,AD平分∠BAC,点D是BC的中点,DM⊥AB,DN⊥AC,垂足分别为M,N,求证:∠B=∠C,BM=CN.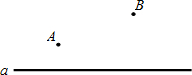 如图,直线a表示一条公路,点A、B表示两个乡镇.如果要在公路旁(直线a上)修一个车站S,使得AS+BS最小,请作出点S.
如图,直线a表示一条公路,点A、B表示两个乡镇.如果要在公路旁(直线a上)修一个车站S,使得AS+BS最小,请作出点S.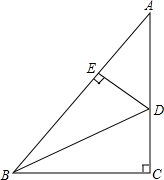 如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,AB=40cm,BC=24cm,S△ABC=384cm2,则DE的长是12cm.
如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,AB=40cm,BC=24cm,S△ABC=384cm2,则DE的长是12cm.