题目内容
17.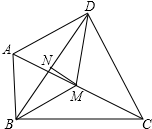 如图,在四边形ABCD中,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,求证:
如图,在四边形ABCD中,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,求证:(1)MD=MB;
(2)MN平分∠DMB.
分析 (1)根据直角三角形斜边上的中线等于斜边的一半可得MB=$\frac{1}{2}$AC,MD=$\frac{1}{2}$AC,然后等量代换即可得证;
(2)根据等腰三角形三线合一的性质证明即可.
解答 证明:(1)∵,∠ABC=∠ADC=90°,M是AC的中点,
∴BM=$\frac{1}{2}$AC,DM=$\frac{1}{2}$AC,
∴MD=MB;
(2)∵MD=MB,N是BD的中点,
∴MN平分∠DMB(等腰三角形三线合一).
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,是基础题,熟记性质是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
7.若关于x的方程ax2-4x-1=0是一元二次方程,则a满足的条件是( )
| A. | a>0 | B. | a≠0 | C. | a<0 | D. | a≠4 |

 如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离5cm,一只蚂蚁如果沿着长方体的表面从A点爬到B点,需要爬行的最短距离是25.
如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离5cm,一只蚂蚁如果沿着长方体的表面从A点爬到B点,需要爬行的最短距离是25.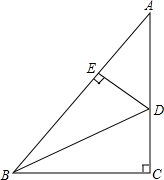 如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,AB=40cm,BC=24cm,S△ABC=384cm2,则DE的长是12cm.
如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,AB=40cm,BC=24cm,S△ABC=384cm2,则DE的长是12cm.