题目内容
18.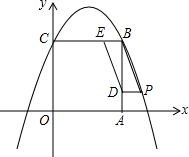 如图,在直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在x轴、y轴的正半轴上.抛物线y=-x2+bx+c经过点B、C.
如图,在直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在x轴、y轴的正半轴上.抛物线y=-x2+bx+c经过点B、C.(1)求抛物线的解析式;
(2)点D、E分别是AB、BC上的动点,且点D从点A开始,以1cm/s的速度沿AB向点B移动,同时点E从点B开始,以1cm/s的速度沿BC向点C移动.运动t 秒(t≤2)后,能否在抛物线上找到一点P,使得四边形BEDP为平行四边形?如果能,请求出t值和点P的坐标;如果不能,请说明理由.
分析 (1)由正方形的性质得到点B、C的坐标,把它们代入抛物线解析式即可求得系数b、c的值;易求抛物线解析式;
(2)由平行四边形的性质得到BE=PD,且BE∥DP,由此得到关于t的方程,通过解方程来求t的值,根据t的值来求点P的坐标.
解答 解:(1)依题意得:B(2,2),C(0,2).
把它们代入y=-x2+bx+c,得
$\left\{\begin{array}{l}{2=-{2}^{2}+2b+c}\\{2=c}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=2}\\{c=2}\end{array}\right.$.
所以,该抛物线的解析式为:y=-x2+2x+2;
(2)∵四边形BEDP为平行四边形,
∴BE=PD,且BE∥DP,
∴设E(2-t,2),则D(2,t),P(2+t,t).
又∵点P在抛物线y=-x2+2x+2上,
∴t=-(2+t)2+2(2+t)+2,
解得:t1=$\frac{-3+\sqrt{17}}{2}$,t2=$\frac{-3-\sqrt{17}}{2}$(负值,舍去).
则2+t=$\frac{1+\sqrt{17}}{2}$,
故点P的坐标为($\frac{1+\sqrt{17}}{2}$,$\frac{-3+\sqrt{17}}{2}$).
点评 本题考查了二次函数综合题.解题时,需要熟练掌握待定系数法求二次函数解析式,正方形的性质,平行四边形的性质以及二次函数图象上点的坐标特征,还要注意“数形结合”的数学思想的应用.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
6.下列各组条件中,能判定△ABC≌△DEF的是( )
| A. | AB=DE,BC=EF,∠A=∠D | B. | ∠A=∠D,∠C=∠F,AC=EF | ||
| C. | AB=DE,BC=EF,AC=DF | D. | ∠B=∠E |
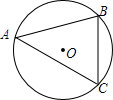 如图,在⊙O中,弦AB=3cm,圆周角∠ACB=60°,则⊙O的直径等于2$\sqrt{3}$cm.
如图,在⊙O中,弦AB=3cm,圆周角∠ACB=60°,则⊙O的直径等于2$\sqrt{3}$cm.