题目内容
15. 如图,⊙O是△ABC的外接圆,弦CD⊥AB,CE是直径,F是弧AB的中点,求证:
如图,⊙O是△ABC的外接圆,弦CD⊥AB,CE是直径,F是弧AB的中点,求证:(1)AC•BC=CE•CD;
(2)CF平分∠ECD.
分析 (1)连接AE,由弦CD⊥AB,CE是直径,得到∠CAE=∠BDC=90°,根据圆周角定理得到∠B=∠E,于是得到△ACE∽△BCD,即可得到结论;
(2)由F是弧AB的中点,得到∠ACF=∠BCF,由(1)知,△ACE∽△BCD,于是得到∠ACE=∠BCD,即可得到结果.
解答  证明:(1)连接AE,
证明:(1)连接AE,
∵弦CD⊥AB,CE是直径,
∴∠CAE=∠BDC=90°,
∵∠B=∠E,
∴△ACE∽△BCD,
∴$\frac{AC}{CD}=\frac{CE}{BC}$,
∴AC•BC=CE•CD;
(2)∵F是弧AB的中点,
∴$\widehat{AF}$=$\widehat{BF}$,
∴∠ACF=∠BCF,
由(1)知,△ACE∽△BCD,
∴∠ACE=∠BCD,
∴∠CEF=∠DCF,
∴CF平分∠ECD.
点评 本题考查了相似三角形的判定和性质,圆周角定理,角平分线的判定,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
6.下列各组条件中,能判定△ABC≌△DEF的是( )
| A. | AB=DE,BC=EF,∠A=∠D | B. | ∠A=∠D,∠C=∠F,AC=EF | ||
| C. | AB=DE,BC=EF,AC=DF | D. | ∠B=∠E |
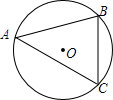 如图,在⊙O中,弦AB=3cm,圆周角∠ACB=60°,则⊙O的直径等于2$\sqrt{3}$cm.
如图,在⊙O中,弦AB=3cm,圆周角∠ACB=60°,则⊙O的直径等于2$\sqrt{3}$cm.

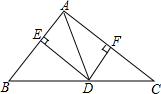 如图,在△ABC中,AB=3cm,AC=4cm,AD是BC的中线,DE,DF分别是△ABD和△ACD的高,求DE:DF的值.
如图,在△ABC中,AB=3cm,AC=4cm,AD是BC的中线,DE,DF分别是△ABD和△ACD的高,求DE:DF的值.