如图.在△ABC中.D.E分别是AB.AC上点.且AE=3.AD=2.DB=4.AB=9.△ADE与△ABC相似吗?为什么? 题目和参考答案——青夏教育精英家教网—

题目内容

1．

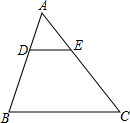如图，在△ABC中，D、E分别是AB、AC上点，且AE=3，AD=2，DB=4，AB=9，△ADE与△ABC相似吗？为什么？

分析先证出两边对应成比例$\frac{AD}{AB}=\frac{AE}{AC}$，再由公共角相等，即可得出结论．

解答解：△ADE∽△ABC，理由如下：
∵AB=AD+DB=2+4=6，
∴$\frac{AD}{AB}$=$\frac{2}{6}$=$\frac{1}{3}$，$\frac{AE}{AC}$=$\frac{3}{9}$=$\frac{1}{3}$，
∴$\frac{AD}{AB}=\frac{AE}{AC}$，
∵∠A=∠A，
∴△ADE∽△ABC．

点评本题考查了相似三角形的判定方法；熟练掌握相似三角形的判定方法，并能进行推理论证是解决问题的关键．

练习册系列答案

12．已知有理数a，b，c，其积是负数，其和是正数，当x=$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}$时，求式子x²⁰¹⁴-2015x+2016的值．

9．用计算器计算并填空．
①11-2=9=（　　）²
②1111-22=1089=（　　）²
③111111一222=110889=（　　）²
④11111111-2222=11108889=（　　）²
（1）你发现了什么规律？
（2）不用计算器，$\underset{\underbrace{111…111}}{2006个}-\underset{\underbrace{222…222}}{1003个}$=（　　）²．

16．函数y=$\frac{8}{x}$与y=x-2图象交点的横坐标分别为a，b，则a+b的值为2．

6．

如图，抛物线顶点坐标是P（1，2），函数y随自变量x的增大而减小的x的取值范围是（　　）

13．在式子$\frac{ab}{3}$，4t²，0，$\frac{1}{x}$，3.5x，m+1，2（a+1），$\frac{3xy}{π}$中，单项式有（　　）

6．下列各组条件中，能判定△ABC≌△DEF的是（　　）

	A．	AB=DE，BC=EF，∠A=∠D		B．	∠A=∠D，∠C=∠F，AC=EF
	C．	AB=DE，BC=EF，AC=DF		D．	∠B=∠E

7．如图，AB∥CD，P为定点，E、F分别是AB、CD上的动点．
（1）求证：∠P=∠BEP+∠PFD；
（2）若M为CD上一点，MN交PF于N．证明：∠PNM=∠NMF+∠NFM；（说明：不能运用三角形内角和定理）
（3）在（2）的基础上，若∠FMN=∠BEP，试说明∠EPF与∠PNM的关系，并证明你的结论．

试题分类