题目内容
19.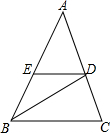 如图,在△ABC中,AB=AC,BD是∠ABC的平分线,DE∥BC,则CD=DE.请说明理由.
如图,在△ABC中,AB=AC,BD是∠ABC的平分线,DE∥BC,则CD=DE.请说明理由.
分析 首先利用DE∥BC,AB=AC,证得∠ADE=∠AED,得出AD=AE,BD=CE,再由BE平分∠ABC,DE∥BC,得出BD=DE,进一步得出结论即可.
解答 证明:∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠C,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ADE=∠AED,
∴AD=AE,
∴BD=CE,
∵BE平分∠ABC,
∴∠DBE=∠EBC,
又∵DE∥BC,
∴∠DEB=∠EBC,
∴∠DBE=∠DEB,
∴BD=DE
∴DE=EC.
点评 此题主要考查等腰三角形的性质,综合利用了平行线的性质和角平分线的定义,掌握基础知识是解决问题的关键

练习册系列答案
相关题目
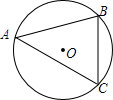 如图,在⊙O中,弦AB=3cm,圆周角∠ACB=60°,则⊙O的直径等于2$\sqrt{3}$cm.
如图,在⊙O中,弦AB=3cm,圆周角∠ACB=60°,则⊙O的直径等于2$\sqrt{3}$cm.
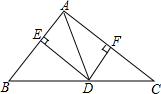 如图,在△ABC中,AB=3cm,AC=4cm,AD是BC的中线,DE,DF分别是△ABD和△ACD的高,求DE:DF的值.
如图,在△ABC中,AB=3cm,AC=4cm,AD是BC的中线,DE,DF分别是△ABD和△ACD的高,求DE:DF的值.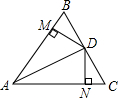 如图所示,△ABC中,AD平分∠BAC,点D是BC的中点,DM⊥AB,DN⊥AC,垂足分别为M,N,求证:∠B=∠C,BM=CN.
如图所示,△ABC中,AD平分∠BAC,点D是BC的中点,DM⊥AB,DN⊥AC,垂足分别为M,N,求证:∠B=∠C,BM=CN.