题目内容
18. 如图,BD平分∠EBC,AD=DC,求证:∠DAB+∠C=180°.
如图,BD平分∠EBC,AD=DC,求证:∠DAB+∠C=180°.
分析 过点D作DF⊥BE于F,作DG⊥BC于G,根据角平分线上的点到角的两边距离相等可得DF=DG,再利用“HL”证明Rt△ADF和Rt△CDG全等,然后根据全等三角形对应角相等可得∠C=∠DAF,然后根据平角等于180°证明即可.
解答  证明:如图,过点D作DF⊥BE于F,作DG⊥BC于G,
证明:如图,过点D作DF⊥BE于F,作DG⊥BC于G,
∵BD平分∠EBC,
∴DF=DG,
在Rt△ADF和Rt△CDG中,$\left\{\begin{array}{l}{AD=DC}\\{DF=DG}\end{array}\right.$,
∴Rt△ADF≌Rt△CDG(HL),
∴∠C=∠DAF,
∵∠DAB+∠DAF=180°,
∴∠DAB+∠C=180°.
点评 本题考查了全等三角形的判定与性质,角平分线上的点到角的两边距离相等的性质,作辅助线构造出全等三角形是解题的关键,也是难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,有一条直的宽纸带,按如图折叠,则∠1的度数为75°.
如图,有一条直的宽纸带,按如图折叠,则∠1的度数为75°.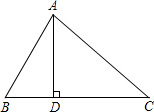 如图,在△ABC中,AD⊥BC于点D,BD=6,AD=6,S△ABC=42,求AC的长.
如图,在△ABC中,AD⊥BC于点D,BD=6,AD=6,S△ABC=42,求AC的长. 如图,在小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
如图,在小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.