题目内容
7．
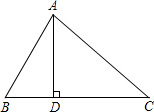如图，在△ABC中，AD⊥BC于点D，BD=6，AD=6，S△ABC=42，求AC的长．
分析 由△ABC的面积求出BC，得出CD，由勾股定理求出AC即可．
解答 解：∵AD⊥BC，
∴∠ADC=90°，S△ABC=$\frac{1}{2}$BC×AD=$\frac{1}{2}$×BC×6=42，
解得：BC=14，
∴CD=BC-BD=14-6=8，
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10．
点评 此题主要考查了勾股定理以及三角形面积的计算；熟练掌握勾股定理，由三角形的面积求出BC是解决问题的关键．
练习册系列答案
应用题作业本系列答案
相关题目
17．抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如表：
由表可知，抛物线与x轴的一个交点是（1，0），则另一个交点的坐标为（ ）
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
| y | … | 5 | 8 | 9 | 8 | 5 | 0 | … |
| A． | （0，5） | B． | （-2，9） | C． | （-5，0） | D． | （2，0） |
如图，BD平分∠EBC，AD=DC，求证：∠DAB+∠C=180°．
15．若不等式组$\left\{\begin{array}{l}{x＜1}\\{x＞-1}\\{x＞m}\end{array}\right.$无解，则m的取值范围是（ ）
| A． | m≤-1 | B． | m≥1 | C． | -1＜m＜1 | D． | m≤-1或m≥1 |
2．在△ABC中，D为BC上一点，且BD=5，AB=13，AD=12，AC=15，则△ABC的面积是（ ）
| A． | 30 | B． | 42 | C． | 84 | D． | 100 |
