题目内容
8.已知点A(1,5),B(4,2),点P在x轴上,当AP+BP最小时,点P的坐标为($\frac{22}{7}$,0).分析 根据轴对称的性质,将A与B的关系转化为A′与B的关系,再根据“两点之间线段最短”连接A′B,将AP+BP转化为A′P+BP,可知A′P与x轴交点即为P点位置,然后求出A'B的解析式,计算出P点坐标即可.
解答 解:作点A关于x轴的对称点A′,连接A′、B,则A′B与x轴相交于点P.
根据“两点之间线段最短”,
设直线解析式为y=kx+b,把A′(1,-5)、B(4,2)分别代入解析式得,
$\left\{\begin{array}{l}{k+b=-5}\\{4k+b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{7}{3}}\\{b=-\frac{22}{3}}\end{array}\right.$,
则解析式为y=$\frac{7}{3}$x-$\frac{22}{3}$,
当y=0时,得x=$\frac{22}{7}$,
于是P($\frac{22}{7}$,0).
故答案为:($\frac{22}{7}$,0).
点评 此题考查轴对称问题,通过轴对称的性质和“两点之间线段最短”找到P点坐标是解题的关键,同时要掌握用待定系数法求函数解析式.

练习册系列答案
相关题目
18.某同学参加射击训练,共射击了六发子弹,击中的环数分别为5,4,9,7,7,10.则下列说法正确的是( )
| A. | 中位数为8 | B. | 方差为 $\frac{13}{3}$ | C. | 众数为10 | D. | 以上均不正确 |
 如图,已知四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E,求证:四边形AMEN是菱形.
如图,已知四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E,求证:四边形AMEN是菱形.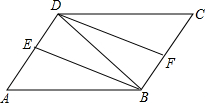 如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:△ABE≌△CDF.
如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:△ABE≌△CDF. 如图,大楼AD与塔CB之间的距离AC长为27m,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶B的仰角为30°,分别求大楼AD的高与塔BC的高(结果精确到0.1m,参考数据:$\sqrt{5}$≈2.24,$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,大楼AD与塔CB之间的距离AC长为27m,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶B的仰角为30°,分别求大楼AD的高与塔BC的高(结果精确到0.1m,参考数据:$\sqrt{5}$≈2.24,$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)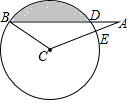 如图,在∠ABC中,∠ACB=130°,∠BAC=20°,BC=4,以点C为圆心,CB长为半径的圆交AB于点D,交AC于点E.
如图,在∠ABC中,∠ACB=130°,∠BAC=20°,BC=4,以点C为圆心,CB长为半径的圆交AB于点D,交AC于点E. 如图,在矩形ABCD中.点E在边AB上,∠CDE=∠DCE.求证:AE=BE.
如图,在矩形ABCD中.点E在边AB上,∠CDE=∠DCE.求证:AE=BE.