题目内容
16.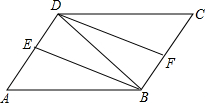 如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:△ABE≌△CDF.
如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:△ABE≌△CDF.
分析 首先利用平行四边形的想得到AB=CD,∠A=∠C,再利用角平分线的性质得到∠ABE=∠CDF,利用ASA证明△ABE≌△CDF.
解答 证明:在?ABCD中,AB=CD,∠A=∠C.
∵AB∥CD,
∴∠ABD=∠CDB.
∵BE平分∠ABD,DF平分∠CDB,
∴∠ABE=$\frac{1}{2}$∠ABD,∠CDF=$\frac{1}{2}$∠CDB.
∴∠ABE=∠CDF.
在△ABE和△CDF中,
∵$\left\{\begin{array}{l}{∠A=∠C}\\{AB=CD}\\{∠ABE=∠CDF}\end{array}\right.$,
∴△ABE≌△CDF.
点评 本题考查全等三角形的判定、平行四边形的性质角平分线的定义,等腰三角形的三线合一等知识,解题的关键是熟练掌握全等三角形的判定方法,属于中考常考题型.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 如图,在平行四边形ABCD中,添加一个条件使它成为一个矩形,你添的条件是AC=BD(不唯一).
如图,在平行四边形ABCD中,添加一个条件使它成为一个矩形,你添的条件是AC=BD(不唯一).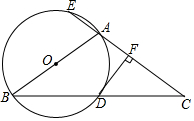 如图,△ABC中,AB=AC,以AB为直径的O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC中,AB=AC,以AB为直径的O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.