题目内容
15.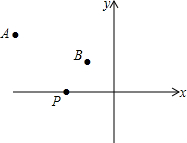 如图,A(-4,2),B(-1,1)在x轴上找一点P,使△PAB的周长最小,求这个最小值及点P的坐标.
如图,A(-4,2),B(-1,1)在x轴上找一点P,使△PAB的周长最小,求这个最小值及点P的坐标.
分析 由于△PAB的周长=PA+AB+PB,而AB是定值,故只需在x轴上找一点P,使PA+PB最小.如果设A关于x轴的对称点为A′,使PA+PB最小就是使PA′+PB最小.
解答 解:作法:作A关于x轴的对称点A′,
连接A′B交x轴于点P.
则点P就是所要求作的点;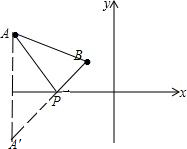
因为A(-4,2),B(-1,1),
所以A'(-4,-2),则可得:A'B=$\sqrt{(-1+4)^{2}+(1+2)^{2}}=3\sqrt{2}$,
设直线A'B的解析式为y=kx+b,
把A'(-4,-2)和B(-1,1)代入可得:$\left\{\begin{array}{l}{-2=-4k+b}\\{1=-k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$,
所以解析式为:y=x+2,
把y=0代入解析式中得:x=-2,
所以点P的坐标为(-2,0).
点评 本题考查了轴对称-最短路线问题解这类问题的关键是把两条线段的和转化为一条线段,运用三角形三边关系解决.

练习册系列答案
相关题目
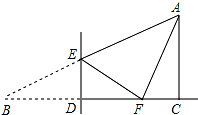 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=6,点D是BC边上一动点(不与B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为直角三角形时,BD的长为1或2.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=6,点D是BC边上一动点(不与B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为直角三角形时,BD的长为1或2.