题目内容
5．计算：（1+$\frac{1}{2}$）（1+$\frac{1}{{2}^{2}}$）（1+$\frac{1}{{2}^{4}}$）（1+$\frac{1}{{2}^{8}}$）=2-$\frac{1}{{2}^{15}}$．分析 原式变形后，利用平方差公式计算即可得到结果．
解答 解：原式=2（1-$\frac{1}{2}$）（1+$\frac{1}{2}$）（1+$\frac{1}{{2}^{2}}$）（1+$\frac{1}{{2}^{4}}$）（1+$\frac{1}{{2}^{8}}$）
=2（1-$\frac{1}{{2}^{2}}$）（1+$\frac{1}{{2}^{2}}$）（1+$\frac{1}{{2}^{4}}$）（1+$\frac{1}{{2}^{8}}$）
=2（1-$\frac{1}{{2}^{4}}$）（1+$\frac{1}{{2}^{4}}$）（1+$\frac{1}{{2}^{8}}$）
=2（1-$\frac{1}{{2}^{8}}$）（1+$\frac{1}{{2}^{8}}$）
=2（1-$\frac{1}{{2}^{16}}$）
=2-$\frac{1}{{2}^{15}}$，
故答案为：2-$\frac{1}{{2}^{15}}$
点评 此题考查了因式分解的应用，熟练掌握平方差公式是解本题的关键．
练习册系列答案
相关题目
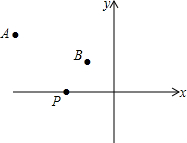如图，A（-4，2），B（-1，1）在x轴上找一点P，使△PAB的周长最小，求这个最小值及点P的坐标．
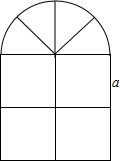窗户的形状如图所示（图中长度单位：cm），其上部是半圆形，下部是边长相同的四个小正方形，已知下部小正方形的边长是a cm，计算：
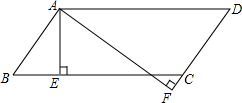如图，在?ABCD中，AE⊥BC于E，AF⊥DC于DC延长线上一点F，AE=3cm，AF=5cm，∠EAF=30°，求?ABCD各角度数、周长及面积．
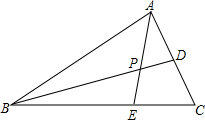如图，在△ABC中，点D、E分别在AC、BC边上，且AD=CD，BE=2CE，AE与BD交于P点．若△ABC的面积为1，求四边形CDPE的面积．
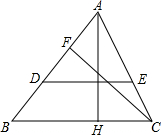如图，在△ABC中，AH⊥BC于H，CF⊥AB于F，D是AB上一点，AD=AH，DE∥BC，求证：DE=CF．