题目内容
20.(1)计算:$\sqrt{20}$+$\sqrt{32}$-($\sqrt{5}$+2$\sqrt{2}$)(2)当x=$\sqrt{5}$-1时,求代数式x2-5x-6的值.
分析 (1)先化成最简二次根式,再合并同类二次根式即可;
(2)先代入,再算乘法,最后合并即可.
解答 解:(1)原式=2$\sqrt{5}$+4$\sqrt{2}$-$\sqrt{5}$-2$\sqrt{2}$
=$\sqrt{5}$+2$\sqrt{2}$;
(2)∵x=$\sqrt{5}$-1,
∴x2-5x-6=($\sqrt{5}$-1)2-5×($\sqrt{5}$-1)-6
=5-2$\sqrt{5}$+1-5$\sqrt{5}$+5-6
=5-7$\sqrt{5}$.
点评 本题考查了二次根式的混合运算的应用,能正确运用二次根式的运算法则进行计算是解此题的关键,注意:运算顺序.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
10.已知下列命题,其中真命题的个数是( )
①若a2=b2,则a=b;
②对角线互相垂直且相等的四边形是正方形;
③两组对角分别相等的四边形是平行四边形;
④在反比例函数y=$\frac{2}{x}$中,如果函数值y<1时,那么自变量x>2.
①若a2=b2,则a=b;
②对角线互相垂直且相等的四边形是正方形;
③两组对角分别相等的四边形是平行四边形;
④在反比例函数y=$\frac{2}{x}$中,如果函数值y<1时,那么自变量x>2.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
5.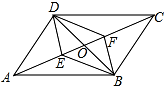 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
9.反比例函数y=$\frac{2}{x}$的图象位于平面直角坐标系的( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一、二象限 | D. | 第三、四象限 |
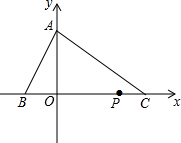 在平面直角坐标中,点A坐标(0,4),点C坐标(6,0),点B在x轴负半轴上,点P从点C出发,以1个单位/秒的速度沿x轴负方向运动,且S△AOC=3S△AOB.
在平面直角坐标中,点A坐标(0,4),点C坐标(6,0),点B在x轴负半轴上,点P从点C出发,以1个单位/秒的速度沿x轴负方向运动,且S△AOC=3S△AOB.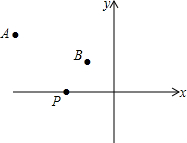 如图,A(-4,2),B(-1,1)在x轴上找一点P,使△PAB的周长最小,求这个最小值及点P的坐标.
如图,A(-4,2),B(-1,1)在x轴上找一点P,使△PAB的周长最小,求这个最小值及点P的坐标.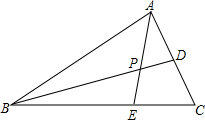 如图,在△ABC中,点D、E分别在AC、BC边上,且AD=CD,BE=2CE,AE与BD交于P点.若△ABC的面积为1,求四边形CDPE的面积.
如图,在△ABC中,点D、E分别在AC、BC边上,且AD=CD,BE=2CE,AE与BD交于P点.若△ABC的面积为1,求四边形CDPE的面积.