题目内容
3.反比例函数y1=$\frac{k}{x}$(x>0,k≠0)的图象进过点(1,3),P点是直线y2=-x+6上一个动点,如图所示,设P点的横坐标为m,且满足-m+6$>\frac{3}{m}$,过P点分别作PB⊥x轴、PA⊥y轴,垂足分别为B、A,与双曲线分别交于D、C两点,连接OC、OD、CD.(1)求k的值并结合图象求出m的取值范围;
(2)在P点运动过程中,求线段OC最短时P点的坐标;
(3)将三角形OCD沿着CD翻折,点O的对应点为O′,得到四边形O′COD,问:四边形O′COD能否为菱形?若能,求出P点坐标;若不能,说明理由.
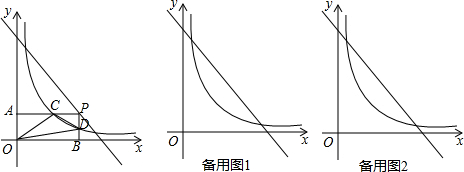
分析 (1)先把(1,3)代入y1=$\frac{k}{x}$求出k的值,再由两函数有交点求出m的值,根据函数图象即可得出结论;
(2)根据线段OC最短可知OC为∠AOB的平分线,对于y1=$\frac{3}{x}$,令x=y1,即可得出C点坐标,把y=$\sqrt{3}$代入y=-x+6中求出x的值即可得出P点坐标;
(3)当OC=OD时,四边形O′COD为菱形,由对称性得到△AOC≌△BOD,即OA=OB,由此时P横纵坐标相等且在直线y=-x+6上即可得出结论.
解答 解:(1)∴反比例函数y1=$\frac{k}{x}$(x>0,k≠0)的图象进过点(1,3),
∴把(1,3)代入y1=$\frac{k}{x}$,解得k=3,
∵$\frac{3}{m}$=-m+6,
∴m=3±$\sqrt{6}$,
∴由图象得:3-$\sqrt{6}$<m<3+$\sqrt{6}$;
(2)∵线段OC最短时,
∴OC为∠AOB的平分线,
∵对于y1=$\frac{3}{x}$,令x=y1,
∴x=$\sqrt{3}$,即C($\sqrt{3}$,$\sqrt{3}$),
∴把y=$\sqrt{3}$代入y=-x+6中,得:x=6-$\sqrt{3}$,即P(6-$\sqrt{3}$,$\sqrt{3}$);
(3)四边形O′COD能为菱形,
∵当OC=OD时,四边形O′COD为菱形,
∴由对称性得到△AOC≌△BOD,即OA=OB,
∴此时P横纵坐标相等且在直线y=-x+6上,即x=-x+6,解得:x=3,即P(3,3).
点评 本题考查的是反比例函数综合题,涉及到菱形的判定与性质、全等三角形的判定与性质等知识,在解答此题时要注意利用数形结合求解.

练习册系列答案
相关题目
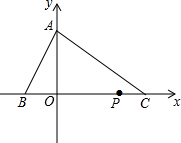 在平面直角坐标中,点A坐标(0,4),点C坐标(6,0),点B在x轴负半轴上,点P从点C出发,以1个单位/秒的速度沿x轴负方向运动,且S△AOC=3S△AOB.
在平面直角坐标中,点A坐标(0,4),点C坐标(6,0),点B在x轴负半轴上,点P从点C出发,以1个单位/秒的速度沿x轴负方向运动,且S△AOC=3S△AOB.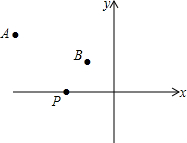 如图,A(-4,2),B(-1,1)在x轴上找一点P,使△PAB的周长最小,求这个最小值及点P的坐标.
如图,A(-4,2),B(-1,1)在x轴上找一点P,使△PAB的周长最小,求这个最小值及点P的坐标.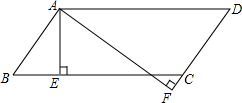 如图,在?ABCD中,AE⊥BC于E,AF⊥DC于DC延长线上一点F,AE=3cm,AF=5cm,∠EAF=30°,求?ABCD各角度数、周长及面积.
如图,在?ABCD中,AE⊥BC于E,AF⊥DC于DC延长线上一点F,AE=3cm,AF=5cm,∠EAF=30°,求?ABCD各角度数、周长及面积.