题目内容
7.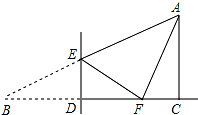 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=6,点D是BC边上一动点(不与B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为直角三角形时,BD的长为1或2.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=6,点D是BC边上一动点(不与B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为直角三角形时,BD的长为1或2.
分析 Rt△ABC中,根据特殊锐角三角函数值可求得AB=4$\sqrt{3}$,然后由翻折的性质可求得∠AEF=60°,从而可求得∠EAF=30°,故此AE=2EF,由翻折的性质可知:BE=EF,故此AB=3BE,所以EB=$\frac{4\sqrt{3}}{3}$,最后在Rt△BED中利用特殊锐角三角函数值即可求得BD的长.当点F在BC的延长线上时,∠AEF=90°,然后依据角平分线的性质可得到ED=AE,然后再证明△BED∽△BAC,最后依据相似三角形的性质求解即可.
解答 解:∵Rt△ABC中,∠ACB=90°,∠B=30°,
∴$\frac{BC}{AB}=\frac{\sqrt{3}}{2}$,即$\frac{6}{AB}=\frac{\sqrt{3}}{2}$.
∴AB=4$\sqrt{3}$
∵∠B=30°,DE⊥BC,
∴∠BED=60°.
由翻折的性质可知:∠BED=∠FED=60°,
∴∠AEF=60°.
∵△AEF为直角三角形,
∴∠EAF=30°.
∴AE=2EF.
由翻折的性质可知:BE=EF,
∴AB=3BE.
∴EB=$\frac{4\sqrt{3}}{3}$.
在Rt△BED中,∠B=30°,
∴$\frac{BD}{BE}=\frac{\sqrt{3}}{2}$,即$\frac{BD}{\frac{4\sqrt{3}}{3}}=\frac{\sqrt{3}}{2}$.
∴BD=2.
如图所示:当点F在BC的延长线上时.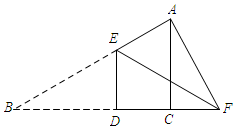
∵△AEF为直角三角形,
∴∠EAF=90°,
∴∠EFA=30°.
∴∠EFD=∠EFA.
又∵ED⊥BF,EA⊥AF,
∴AE=DE.
∵BC=6,∠ACB=90°,∠B=30°,
∴AB=4$\sqrt{3}$,AC=2$\sqrt{3}$
设DE=x,BE=4$\sqrt{3}$-x.
∵DE∥AC,
∴$\frac{ED}{AC}=\frac{BE}{AB}$,$\frac{x}{2\sqrt{3}}=\frac{4\sqrt{3}-x}{4\sqrt{3}}$,解得:x=1.
故答案为:1或2.
点评 本题主要考查的是翻折的性质和特殊锐角三角函数值的应用,掌握翻折的性质和特殊锐角三角函数值是解题的关键.

| A. | 缩小为原来的$\frac{1}{2}$ | B. | 缩小为原来的$\frac{1}{4}$ | C. | 分式的值不变 | D. | 扩大为原来的2倍 |
| A. | x2-8=0 | B. | 2x2-4x+3=0 | C. | 9x2+6x+1=0 | D. | 5x+2=3x2 |
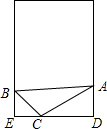 小明将斜边AB=1米的直角三角形按图所示放置,其中∠BAC=30°,∠ACB=90°,∠ACD=37°,请你帮小明计算此门的宽度DE(参考数据:sin37°≈0.6,cos37°≈0.8,$\sqrt{3}$≈1.73,结果精确到0.01米)
小明将斜边AB=1米的直角三角形按图所示放置,其中∠BAC=30°,∠ACB=90°,∠ACD=37°,请你帮小明计算此门的宽度DE(参考数据:sin37°≈0.6,cos37°≈0.8,$\sqrt{3}$≈1.73,结果精确到0.01米)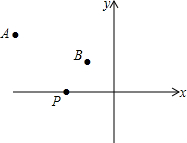 如图,A(-4,2),B(-1,1)在x轴上找一点P,使△PAB的周长最小,求这个最小值及点P的坐标.
如图,A(-4,2),B(-1,1)在x轴上找一点P,使△PAB的周长最小,求这个最小值及点P的坐标.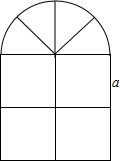 窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长是a cm,计算:
窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长是a cm,计算: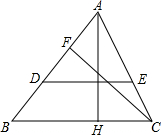 如图,在△ABC中,AH⊥BC于H,CF⊥AB于F,D是AB上一点,AD=AH,DE∥BC,求证:DE=CF.
如图,在△ABC中,AH⊥BC于H,CF⊥AB于F,D是AB上一点,AD=AH,DE∥BC,求证:DE=CF.