题目内容
20.二次函数y=x2-bx+b-2图象与x轴交于点A(x1,0),B(x2,0),且0<x1<1,2<x2<3,则满足条件的b的取值可能是( )| A. | -2或3 | B. | 2.5或3.6 | C. | 3或2.5 | D. | 4或-1 |
分析 依照题意画出函数图象,利用数形结合即可得出关于b的一元一次不等式组,解之即可得出b的取值范围,再对照四个选项即可得出结论.
解答 解:依照题意画出函数图象,如图所示.
观察函数图象可知:$\left\{\begin{array}{l}{b-2>0}\\{1-b+b-2<0}\\{4-2b+b-2<0}\\{9-3b+b-2>0}\end{array}\right.$,
解得:2<b<$\frac{7}{2}$.
故选C.
点评 本题考查了抛物线与x轴的交点、二次函数的图象以及解一元一次不等式组,依照题意画出函数图象,利用数形结合找出关于b的一元一次不等式组是解题的关键.

练习册系列答案
相关题目
5.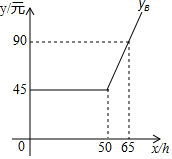 某网站策划了A、B两种上网的月收费方式:
某网站策划了A、B两种上网的月收费方式:
设每月上网学习时间为x(h)小时,方案A,B的收费金额分别为yA (元)、yB(元).
如图是yB与x之间函数关系的图象
(友情提示:若累计上网时间不超出“包时上网时间”,则只收”月使用费“;若累计上网时间不超出“包时上网时间”,则对超出部分再加收”超时费“)
(1)m=45;n=50p=0.05.
(2)写出yA与x之间的函数关系式.
(3)若每月上网的时间为29小时,请说明选取哪种方式能节省上网费?
 某网站策划了A、B两种上网的月收费方式:
某网站策划了A、B两种上网的月收费方式:| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
| A | 30 | 25 | 0.05 |
| B | m | n | P |
如图是yB与x之间函数关系的图象
(友情提示:若累计上网时间不超出“包时上网时间”,则只收”月使用费“;若累计上网时间不超出“包时上网时间”,则对超出部分再加收”超时费“)
(1)m=45;n=50p=0.05.
(2)写出yA与x之间的函数关系式.
(3)若每月上网的时间为29小时,请说明选取哪种方式能节省上网费?
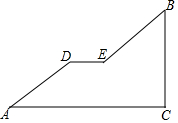 如图是一座人行天桥引桥部分的示意图,上桥通道由两段互相平行并且与地面成37°角楼梯AD,BE和一段水平平台DE构成.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图是一座人行天桥引桥部分的示意图,上桥通道由两段互相平行并且与地面成37°角楼梯AD,BE和一段水平平台DE构成.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)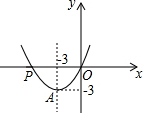 已知抛物线y=ax2+bx经过点A(-3,-3)和点P(m,0),且m≠0.
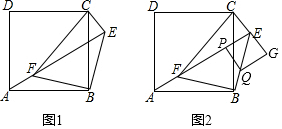
已知抛物线y=ax2+bx经过点A(-3,-3)和点P(m,0),且m≠0.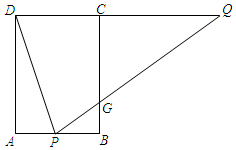 如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.
如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.
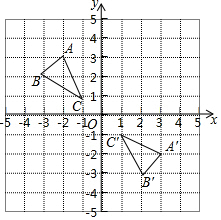 如图,在平面直角坐标系中,△ABC的顶点坐标为A(-2,3)、B(-3,2)、C(-1,1)
如图,在平面直角坐标系中,△ABC的顶点坐标为A(-2,3)、B(-3,2)、C(-1,1)