题目内容
15.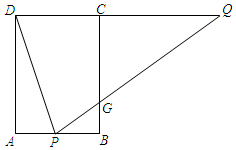 如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.
如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.(1)求证:DQ=PQ;
(2)求AP•DQ的最大值;
(3)若P为AB的中点,求PG的长.
分析 (1)欲推知DQ=PQ,只需得到∠QPD=∠QDP,结合矩形的性质和平行线的性质就可得到该结论;
(2)由相似三角形△QDE∽△DPA的对应边成比例推知:AP•DQ=DP•DE=$\frac{1}{2}$DP2.结合Rt△DAP中,利用勾股定理得到:AP•DQ=$\frac{1}{2}$(36+AP2),由AP的取值范围;
(3)设CG=x,则BG=6-x,由(1)得,DQ∥AB,所以由平行线分线段成比例得到$\frac{CQ}{BP}$=$\frac{CG}{BG}$,即$\frac{6}{2}$=$\frac{x}{6-x}$,由此求得x的值,进而结合勾股定理得到PG的长度.
解答  (1)证明:∵四边形ABDF是矩形,
(1)证明:∵四边形ABDF是矩形,
∴AB∥CD,
∴∠APD=∠QDP.
∵∠APD=∠QPD,
∴∠QPD=∠QDP,
∴DQ=PQ.
(2)过点Q作QE⊥DP,垂足为E,则DE=$\frac{1}{2}$DP.
∵∠DEQ=∠PAD=90°,∠QDP=∠APD,
∴△QDE∽△DPA,
∴$\frac{DQ}{DP}$=$\frac{DE}{AP}$,
∴AP•DQ=DP•DE=$\frac{1}{2}$DP2.
在Rt△DAP中,有DP2=DA2+AP2=36+AP2,
∴AP•DQ=$\frac{1}{2}$(36+AP2),
∵点P在AB上,
∴AP≤4,
∴AP•DQ≤26,即AP•DQ的最大值为26.
(3)∵P为AB的中点,
∴AP=BP=$\frac{1}{2}$AB=2,
由(2)得,DQ=$\frac{1}{4}$(36+22)=10.
∴CQ=DQ-DC=6.设CG=x,则BG=6-x,
由(1)得,DQ∥AB,
∴$\frac{CQ}{BP}$=$\frac{CG}{BG}$,
即$\frac{6}{2}$=$\frac{x}{6-x}$,
解得x=$\frac{9}{2}$,
∴BG=6-$\frac{9}{2}$=$\frac{3}{2}$,
∴PG=$\sqrt{P{B}^{2}+B{G}^{2}}$=$\frac{5}{2}$.
点评 本题考查了相似综合题,需要熟练掌握矩形的性质,平行线分线段成比例,勾股定理以及相似三角形的判定与性质,综合性较强,属于难题.

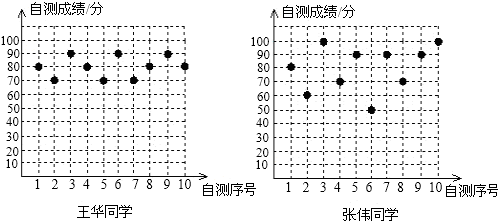
(1)根据图中提供的数据列出如下统计表:
| 平均成绩(分) | 中位数(分) | 众数(分) | 方差(S2) | |
| 王华 | 80 | b | 80 | d |
| 张伟 | a | 85 | c | 260 |
(2)将90分以上(含90分)的成绩视为优秀,则优秀率高的是张伟.
(3)现在要从这两个同学选一位去参加数学竞赛,你可以根据以上的数据给老师哪些建议?
| A. | -2或3 | B. | 2.5或3.6 | C. | 3或2.5 | D. | 4或-1 |
| A. | 正五边形是中心对称图形 | |
| B. | 平分弦的直径垂直于弦 | |
| C. | 化简-a$\sqrt{-\frac{1}{a}}$的结果是$\sqrt{-a}$ | |
| D. | 顺次连接对角线互相垂直的四边形各边中点所得的四边形是菱形 |
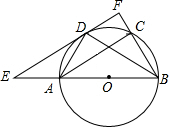 如图,AB为⊙O的直径,C、D为⊙O上的两点,且D为弧AC的中点,过点D作EF∥AC分别交直线AB,BC于点E、F,AC=6,BD=5.
如图,AB为⊙O的直径,C、D为⊙O上的两点,且D为弧AC的中点,过点D作EF∥AC分别交直线AB,BC于点E、F,AC=6,BD=5. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P从点A出发沿边AC向点C以每秒1个单位长度的速度运动,同时点Q从点C出发沿边CB向点B以每秒a个单位长度的速度运动,过点P作PD⊥BC,交AB于点D,连接PQ.当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P从点A出发沿边AC向点C以每秒1个单位长度的速度运动,同时点Q从点C出发沿边CB向点B以每秒a个单位长度的速度运动,过点P作PD⊥BC,交AB于点D,连接PQ.当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).