题目内容
8.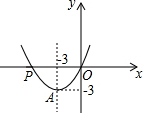 已知抛物线y=ax2+bx经过点A(-3,-3)和点P(m,0),且m≠0.
已知抛物线y=ax2+bx经过点A(-3,-3)和点P(m,0),且m≠0.(1)如图,若该抛物线的对称轴经过点A,求此时y的最小值和m的值.
(2)若m=-2时,设此时抛物线的顶点为B,求四边形OAPB的面积.
分析 (1)直接利用二次函数图象得出其最值以及m的值;
(2)利用待定系数法求出a,b的值,进而求得点B的坐标,利用三角形面积公式,即可得出四边形OAPB的面积.
解答 解:(1)根据题意得:A是抛物线的顶点,
∴此时y的最小值-3,对称轴是直线x=-3,
∴m=-6.
(2)将(-2,0)、(-3,-3)代入y=ax2+bx中,
$\left\{\begin{array}{l}{4a-2b=0}\\{9a-3b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=-2}\end{array}\right.$.
∴抛物线解析式为y=-x2-2x=-(x+1)2+1,
∴抛物线顶点B(-1,1).
∴S四边形OAPB=S△OPA+S△OPA=$\frac{1}{2}$×2×1+$\frac{1}{2}$×2×3=4.
∴四边形OAPB的面积是4.
点评 此题主要考查了二次函数的性质以及待定系数法求出二次函数解析式,解题的关键是:(1)根据二次函数的性质找出点A为抛物线的顶点;(2)根据点的坐标,利用待定系数法求出二次函数解析式.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
13.小洪根据演讲比赛中九位评委所给的分数制作了如表:
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是中位数.
| 平均数 | 中位数 | 众数 | 方差 |
| 8.5 | 8.3 | 8.1 | 0.15 |
20.二次函数y=x2-bx+b-2图象与x轴交于点A(x1,0),B(x2,0),且0<x1<1,2<x2<3,则满足条件的b的取值可能是( )
| A. | -2或3 | B. | 2.5或3.6 | C. | 3或2.5 | D. | 4或-1 |
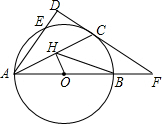 如图,AB是⊙O的直径,C为⊙O上一点,AD与过C点的切线垂直,垂足为D,AD交⊙O于E,DE=2,CD=4.
如图,AB是⊙O的直径,C为⊙O上一点,AD与过C点的切线垂直,垂足为D,AD交⊙O于E,DE=2,CD=4.