题目内容
11.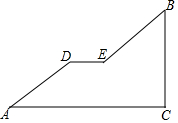 如图是一座人行天桥引桥部分的示意图,上桥通道由两段互相平行并且与地面成37°角楼梯AD,BE和一段水平平台DE构成.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图是一座人行天桥引桥部分的示意图,上桥通道由两段互相平行并且与地面成37°角楼梯AD,BE和一段水平平台DE构成.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
分析 首先由已知构造直角三角形如图,延长BE交AC于F,过点E作EG⊥AC,垂足为G,解直角三角形BCF求得CF,又由已知BE∥AD,四边形AFED为平行四边形,所以DE=AF=AC-CF.
解答  解:(1)延长BE交AC于F,过点E作EG⊥AC,垂足为G,
解:(1)延长BE交AC于F,过点E作EG⊥AC,垂足为G,
在Rt△BCF中,
CF=$\frac{BC}{tan37°}$=$\frac{4.8}{0.75}$=6.4(米),
∴AF=AC-CF=8-6.4=1.6(米),
∵BE∥AD,
∴四边形AFED为平行四边形,
∴DE=AF=1.6米.
答:水平平台DE的长度为1.6米.
点评 此题考查的知识点是解直角三角形的应用,关键是由已知首先构建直角三角形,运用三角函数求解.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
20.二次函数y=x2-bx+b-2图象与x轴交于点A(x1,0),B(x2,0),且0<x1<1,2<x2<3,则满足条件的b的取值可能是( )
| A. | -2或3 | B. | 2.5或3.6 | C. | 3或2.5 | D. | 4或-1 |
1.下列各式计算正确的是( )
| A. | x2•x3=x6 | B. | 2x+3x=5x2 | C. | x6÷x2=x3 | D. | (x2)3=x6 |
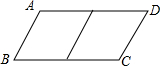 邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图,?ABCD中,若AB=1,BC=2,则□ABCD为1阶准菱形.
邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图,?ABCD中,若AB=1,BC=2,则□ABCD为1阶准菱形.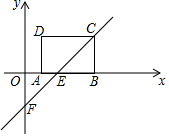 如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x-2与x轴、y轴分别交于点E、F.
如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x-2与x轴、y轴分别交于点E、F.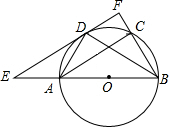 如图,AB为⊙O的直径,C、D为⊙O上的两点,且D为弧AC的中点,过点D作EF∥AC分别交直线AB,BC于点E、F,AC=6,BD=5.
如图,AB为⊙O的直径,C、D为⊙O上的两点,且D为弧AC的中点,过点D作EF∥AC分别交直线AB,BC于点E、F,AC=6,BD=5.