题目内容
16.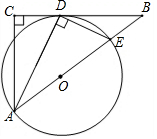 已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.
已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.(1)求证:BC是⊙O的切线;
(2)若AC=3,BC=4,求BE的长.
分析 (1)连接OD,由AE为直径、DE⊥AD可得出点D在⊙O上且∠DAO=∠ADO,根据AD平分∠CAB可得出∠CAD=∠DAO=∠ADO,由“内错角相等,两直线平行”可得出AC∥DO,再结合∠C=90°即可得出∠ODB=90°,进而即可证出BC是⊙O的切线;
(2)在Rt△ACB中,利用勾股定理可求出AB的长度,设OD=r,则BO=5-r,由OD∥AC可得出$\frac{DO}{AC}$=$\frac{BO}{BA}$,代入数据即可求出r值,再根据BE=AB-AE即可求出BE的长度.
解答 (1)证明:连接OD,如图所示.
在Rt△ADE中,点O为AE的中心,
∴DO=AO=EO=$\frac{1}{2}$AE,
∴点D在⊙O上,且∠DAO=∠ADO.
又∵AD平分∠CAB,
∴∠CAD=∠DAO,
∴∠ADO=∠CAD,
∴AC∥DO.
∵∠C=90°,
∴∠ODB=90°,即OD⊥BC.
又∵OD为半径,
∴BC是⊙O的切线;
(2)解:∵在Rt△ACB中,AC=3,BC=4,
∴AB=5.
设OD=r,则BO=5-r.
∵OD∥AC,
∴△BDO∽△BCA,
∴$\frac{DO}{AC}$=$\frac{BO}{BA}$,即$\frac{r}{3}$=$\frac{5-r}{5}$,
解得:r=$\frac{15}{8}$,
∴BE=AB-AE=5-$\frac{15}{4}$=$\frac{5}{4}$.
点评 本题考查了切线的判定与性质、相似三角形的判定与性质、平行线的判定与性质以及勾股定理,解题的关键是:(1)利用平行线的性质找出OD⊥BC;(2)利用相似三角形的性质求出⊙O的半径.

练习册系列答案
相关题目
7. 如图,直线ι是一次函数y=kx+b的图象,若点A(3,m)在直线ι上,则m的值是( )
如图,直线ι是一次函数y=kx+b的图象,若点A(3,m)在直线ι上,则m的值是( )
 如图,直线ι是一次函数y=kx+b的图象,若点A(3,m)在直线ι上,则m的值是( )
如图,直线ι是一次函数y=kx+b的图象,若点A(3,m)在直线ι上,则m的值是( )| A. | -5 | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | 7 |
4.一年之中地球与太阳之间的距离随时间而变化,1个天文单位是地球与太阳之间的平均距离,即1.4960亿km,用科学记数法表示1个天文单位是( )
| A. | 14.960×107km | B. | 1.4960×108km | C. | 1.4960×109km | D. | 0.14960×109km |
10.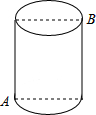 如图,一圆柱高8cm,底面周长为30cm,一只蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )
如图,一圆柱高8cm,底面周长为30cm,一只蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )
 如图,一圆柱高8cm,底面周长为30cm,一只蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )
如图,一圆柱高8cm,底面周长为30cm,一只蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )| A. | 30 cm | B. | 18 cm | C. | 17 cm | D. | 15 cm |
 如图,AD与BE相交于F,∠A=∠C,∠1与∠2互补.
如图,AD与BE相交于F,∠A=∠C,∠1与∠2互补.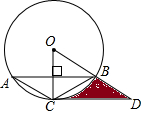 已知:如图,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由$\widehat{BC}$,线段CD和线段BD所围成图形的阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
已知:如图,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由$\widehat{BC}$,线段CD和线段BD所围成图形的阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.