题目内容
11.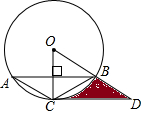 已知:如图,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由$\widehat{BC}$,线段CD和线段BD所围成图形的阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
已知:如图,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由$\widehat{BC}$,线段CD和线段BD所围成图形的阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
分析 根据圆周角定理和垂径定理得到∠O=60°,$\widehat{AC}$=$\widehat{BC}$,根据等腰三角形的性质得到∠ABC=∠A=30°,得到∠OCB=60°,解直角三角形得到CD=$\sqrt{3}$OC=2$\sqrt{3}$,于是得到结论.
解答 解:∵OC⊥AB,∠A=∠BCD=30°,AC=2,
∴∠O=60°,$\widehat{AC}$=$\widehat{BC}$,
∴AC=BC=6,
∴∠ABC=∠A=30°,
∴∠OCB=60°,
∴∠OCD=90°,
∴OC=BC=2,
∴CD=$\sqrt{3}$OC=2$\sqrt{3}$,
∴线段CD和线段BD所围成图形的阴影部分的面积=S△OCD-S扇形BOC-$\frac{1}{2}×$2×2$\sqrt{3}$-$\frac{60•π×{2}^{2}}{360}$=2$\sqrt{3}$-$\frac{2}{3}$π,
故答案为:2$\sqrt{3}$-$\frac{2}{3}$π.
点评 本题考查了扇形的面积的计算,圆周角定理,垂径定理,等边三角形的判定和性质,正确的识别图形是解题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
19.下列运算正确的是( )
| A. | 4x+5y=9xy | B. | (-m)3•m7=m10 | C. | (x2y)5=x2y5 | D. | a12÷a8=a4 |
6.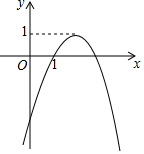 在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,则下列结论正确的是( )
在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,则下列结论正确的是( )
 在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,则下列结论正确的是( )
在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,则下列结论正确的是( )| A. | a<0,b<0,c>0 | |
| B. | -$\frac{b}{2a}$=1 | |
| C. | a+b+c<0 | |
| D. | 关于x的方程ax2+bx+c=-1有两个不相等的实数根 |
4.若n(n≠0)是关于x的方程x2-mx+2n=0的根,则m-n的值为( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
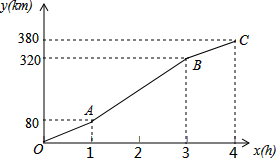 暑假期间,小刚一家乘车去离家380km的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
暑假期间,小刚一家乘车去离家380km的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示. 如图所示,正方形ABCD的边长为4,AD∥y轴,D(1,-1)
如图所示,正方形ABCD的边长为4,AD∥y轴,D(1,-1)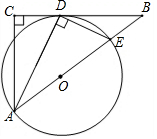 已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.
已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.