题目内容
5.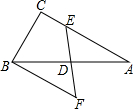 如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥C交ED延长线于点F,则四边形BCEF周长的最小值为( )
如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥C交ED延长线于点F,则四边形BCEF周长的最小值为( )| A. | 1+$\sqrt{3}$ | B. | 4 | C. | 2+$\sqrt{3}$ | D. | 2+$\frac{2\sqrt{3}}{3}$ |
分析 由△ADE≌△BDF,推出BF=AE,推出四边形BCEF的周长=BC+CE+EF+BF=BC+AC+EF,由题意易知BC=1,AC=$\sqrt{3}$,即可推出EF最小时,四边形BCEF的周长最小,当DE⊥AC时,EF的值最小.
解答 解: ∵BF∥AC,
∵BF∥AC,
∴∠A=∠FBD,
在△ADE和△BDF中,
$\left\{\begin{array}{l}{∠A=∠FBD}\\{∠EDA=∠BDF}\\{AD=BD}\end{array}\right.$,
∴△ADE≌△BDF,
∴BF=AE,
∴四边形BCEF的周长=BC+CE+EF+BF=BC+AC+EF,
由题意易知BC=1,AC=$\sqrt{3}$,
∴EF最小时,四边形BCEF的周长最小,当DE⊥AC时,EF的值最小,
∵BD=AD,DE∥CB,
∴CE=AE,
∴DE=$\frac{1}{2}$BC=$\frac{1}{2}$,
∴EF=2DE=1,
∴四边形BCEF周长的最小值为2+$\sqrt{3}$,
点评 本题考查全等三角形的判定和性质、垂线段最短、时间最的中位线定理等知识,解题的关键是正确寻找全等三角形解决问题,学会利用垂线段最短解决最值问题,属于中考常考题型.

练习册系列答案
相关题目
15.下列4个图形中,是中心对称图形但不是轴对称的图形是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.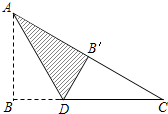 如图,Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在斜边AC上,与点B′重合,AD为折痕,求DB′的长.
如图,Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在斜边AC上,与点B′重合,AD为折痕,求DB′的长.