题目内容
17.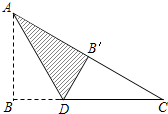 如图,Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在斜边AC上,与点B′重合,AD为折痕,求DB′的长.
如图,Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在斜边AC上,与点B′重合,AD为折痕,求DB′的长.
分析 根据勾股定理得到AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,由折叠的性质得到AB′=AB=3,DB′=BD,∠AB′D=∠CB′D=90°,设B′D=BD=x,则CD=4-x,根据勾股定理即可得到结论.
解答 解:在Rt△ABC中,∠B=90°,AB=3,BC=4,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,
∵将△ABC折叠,使点B恰好落在斜边AC上,与点B′重合,
∴AB′=AB=3,DB′=BD,∠AB′D=∠CB′D=90°,
∴CB′=2,
设B′D=BD=x,则CD=4-x,
∵DB′2+CB′2=CD2,
∴x2+22=(4-x)2,
解得x=$\frac{3}{2}$,
∴DB′=$\frac{3}{2}$.
点评 本题考查了翻折变换-折叠问题,勾股定理,熟练掌握折叠的性质是解题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
5.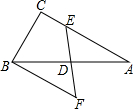 如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥C交ED延长线于点F,则四边形BCEF周长的最小值为( )
如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥C交ED延长线于点F,则四边形BCEF周长的最小值为( )
 如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥C交ED延长线于点F,则四边形BCEF周长的最小值为( )
如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥C交ED延长线于点F,则四边形BCEF周长的最小值为( )| A. | 1+$\sqrt{3}$ | B. | 4 | C. | 2+$\sqrt{3}$ | D. | 2+$\frac{2\sqrt{3}}{3}$ |
6.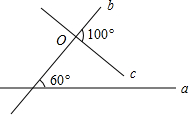 平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a垂直,则旋转的最小度数是( )
平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a垂直,则旋转的最小度数是( )
 平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a垂直,则旋转的最小度数是( )
平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a垂直,则旋转的最小度数是( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
7.一张矩形纸片ABCD,已知AB=3,AD=2,小明按如图步骤折叠纸片,则线段DG长为( )
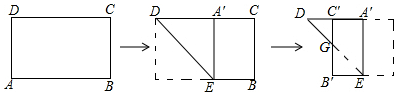

| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 1 | D. | 2 |
 如图,将一张长方形纸片ABCD沿EF折叠,使C,D分别在C′,D′处,C′E交AF于点G,且∠CEF=65°,求∠GFD′的度数.
如图,将一张长方形纸片ABCD沿EF折叠,使C,D分别在C′,D′处,C′E交AF于点G,且∠CEF=65°,求∠GFD′的度数.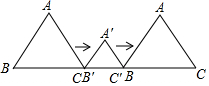 如图,边长为4的等边△ABC和边长为2的等边△A′B′C′的位置如图所示,它们的边BC、B′C′位于同一条直线l上,点C与B′重合,△A′B′C′固定不动,然后把△ABC自左向右沿直线l平移,移出△A′B′C′外(点B与C′重合)停止,设△ABC平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )
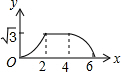
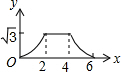
如图,边长为4的等边△ABC和边长为2的等边△A′B′C′的位置如图所示,它们的边BC、B′C′位于同一条直线l上,点C与B′重合,△A′B′C′固定不动,然后把△ABC自左向右沿直线l平移,移出△A′B′C′外(点B与C′重合)停止,设△ABC平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )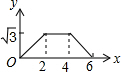
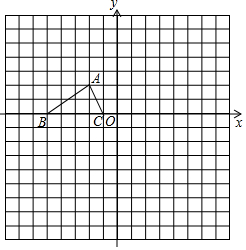 如图,已知△ABC的三个顶点的坐标分别为A(-2,2)、B(-5,0)、C(-1,0),P(a,b)是△ABC的边AC上一点:
如图,已知△ABC的三个顶点的坐标分别为A(-2,2)、B(-5,0)、C(-1,0),P(a,b)是△ABC的边AC上一点: