题目内容
13.为了迎接校运会开幕式,现要求甲乙两队赶制小红旗,已知甲队的工作效率是乙队的2倍,若两队各单独赶制400面小红旗,甲队比乙队少用4天完成.(1)问甲、乙两队每天各能制作多少面小红旗?
(2)已知甲队、乙队每天的制作费用分别是400元、250元,若要制作的小红旗的数量为1800面,且总费用不超过8000元,问至少应安排甲队制作多少天?
分析 (1)设乙队每天制作x面小红旗,则甲队每天制作2x面小红旗,根据两队各单独赶制400面小红旗,甲队比乙队少用4天完成,列出方程求解即可;
(2)设安排甲队制作y天,根据要制作的小红旗的数量为1800面,且总费用不超过8000元,列出不等式,求解即可.
解答 解:(1)设乙队每天制作x面小红旗,则甲队每天制作2x面小红旗,依题意得:
$\frac{400}{x}$-$\frac{400}{2x}$=4,
解得:x=50,经检验,x=50是原方程的根,且符合题意,
答:甲、乙两队每天分别能制作100面、50面小红旗.
(2)设安排甲队制作y天,依题意得:
400y+250×$\frac{1800-100y}{50}$≤8000,
解得:y≥10.
答:至少应安排甲队制作10天.
点评 此题考查了分式方程的应用和一元一次不等式的应用,根据题意准确抓住相等关系或不等关系是解题的根本和关键.

练习册系列答案
相关题目
4.某蔬菜基地打算将115吨的蔬菜运往县城销售,现找到一物流公司有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示(假设每辆车均满载,并且每种车型数量足够):
(1)若全部蔬菜都用甲、乙两种车型来运送,需运费7800元,问分别需甲、乙两种车型各几辆?
(2)蔬菜基地计划用甲、乙、丙三种车型共15辆同时参与运送,将全部蔬菜运往县城销售,如何安排装运,可使运费最省?最省运费是多少?
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
(2)蔬菜基地计划用甲、乙、丙三种车型共15辆同时参与运送,将全部蔬菜运往县城销售,如何安排装运,可使运费最省?最省运费是多少?
5.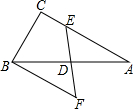 如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥C交ED延长线于点F,则四边形BCEF周长的最小值为( )
如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥C交ED延长线于点F,则四边形BCEF周长的最小值为( )
 如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥C交ED延长线于点F,则四边形BCEF周长的最小值为( )
如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥C交ED延长线于点F,则四边形BCEF周长的最小值为( )| A. | 1+$\sqrt{3}$ | B. | 4 | C. | 2+$\sqrt{3}$ | D. | 2+$\frac{2\sqrt{3}}{3}$ |
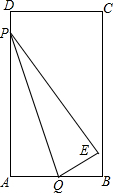 如图,矩形纸ABCD,AB=3,AD=6,动点Q从点A出发以每秒1个单位长的速度沿AB向终点B运动,运动$\frac{2}{3}$秒时,动点P从点D出发以相等的速度沿DA向终点A运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).将△APQ沿PQ翻折,得到△EPQ
如图,矩形纸ABCD,AB=3,AD=6,动点Q从点A出发以每秒1个单位长的速度沿AB向终点B运动,运动$\frac{2}{3}$秒时,动点P从点D出发以相等的速度沿DA向终点A运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).将△APQ沿PQ翻折,得到△EPQ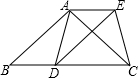 已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.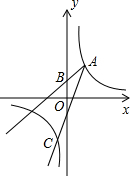 如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=$\frac{k}{x}$的图象上,作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为(-1,-6).
如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=$\frac{k}{x}$的图象上,作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为(-1,-6).