题目内容
14.我区某校为了更好地开展学生课外体育运动,学校决定用1600元购进排球8个,篮球14个,已知每个篮球的售价比排球的售价多20元.(1)每个排球、篮球的售价分别为多少元;
(2)若学校打算再次购进两种球共30个,且购买的30个球中排球的总金额不低于篮球的总金额,若排球、篮球的进价分别为50元、65元,则在第二次购买活动中,商家最多能获利多少?
分析 (1)设排球的单价为x元,则篮球的单价为(x+20)元,则根据所花的钱数为1600元,可得出方程,解出即可;
(2)设购买排球a个,则篮球(30-a)个,根据题意可得出不等式,60a≥80(30-a)可得a的取值范围,设在第二次购买活动中,商家最多能获利w元,可得出w与a的函数关系式,可得a和w的值.
解答 解:(1)设排球的单价为x元,则篮球的单价为(x+20)元,
根据题意,得8x+14(x+20)=1600,
解得:x=60,x+20=80.
答:排球的单价为60元,则篮球的单价为80元;
(2)设购买排球a个,则篮球(30-a)个,
据题意得,60a≥80(30-a)
解得a≥17$\frac{1}{7}$;
设在第二次购买活动中,商家最多能获利w元,则有w=10a+15(30-a)=-5a+450
∵-5<0,w随x的增大而减少,且a为整数,
∴当a=18时,w最大值为360元.
点评 此题考查了一元一次方程及一元一次不等式组的应用,解答本题的关键是仔细审题,根据题意所述的等量关系及不等关系,列出不等式,难度一般.

练习册系列答案
相关题目
4.某蔬菜基地打算将115吨的蔬菜运往县城销售,现找到一物流公司有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示(假设每辆车均满载,并且每种车型数量足够):
(1)若全部蔬菜都用甲、乙两种车型来运送,需运费7800元,问分别需甲、乙两种车型各几辆?
(2)蔬菜基地计划用甲、乙、丙三种车型共15辆同时参与运送,将全部蔬菜运往县城销售,如何安排装运,可使运费最省?最省运费是多少?
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
(2)蔬菜基地计划用甲、乙、丙三种车型共15辆同时参与运送,将全部蔬菜运往县城销售,如何安排装运,可使运费最省?最省运费是多少?
5.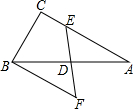 如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥C交ED延长线于点F,则四边形BCEF周长的最小值为( )
如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥C交ED延长线于点F,则四边形BCEF周长的最小值为( )
 如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥C交ED延长线于点F,则四边形BCEF周长的最小值为( )
如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥C交ED延长线于点F,则四边形BCEF周长的最小值为( )| A. | 1+$\sqrt{3}$ | B. | 4 | C. | 2+$\sqrt{3}$ | D. | 2+$\frac{2\sqrt{3}}{3}$ |
19.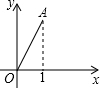 如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )
如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )
 如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )
如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )| A. | (0,2) | B. | (0,-2) | C. | (-1,-$\sqrt{3}$) | D. | ($\sqrt{3}$,1) |
6.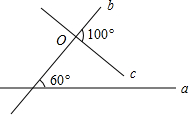 平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a垂直,则旋转的最小度数是( )
平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a垂直,则旋转的最小度数是( )
 平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a垂直,则旋转的最小度数是( )
平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a垂直,则旋转的最小度数是( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
4. 小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是( )
小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是( )
 小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是( )
小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是( )| A. | (-2,1) | B. | (-1,1) | C. | (1,-2) | D. | (-1,-2) |
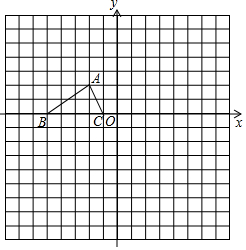 如图,已知△ABC的三个顶点的坐标分别为A(-2,2)、B(-5,0)、C(-1,0),P(a,b)是△ABC的边AC上一点:
如图,已知△ABC的三个顶点的坐标分别为A(-2,2)、B(-5,0)、C(-1,0),P(a,b)是△ABC的边AC上一点: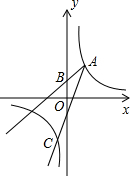 如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=$\frac{k}{x}$的图象上,作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为(-1,-6).
如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=$\frac{k}{x}$的图象上,作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为(-1,-6).