题目内容
17.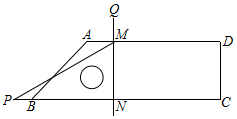 已知四边形ABCD,∠ABC=45°,∠C=∠D=90°,含30°角(∠P=30°)的直角三角板PMN(如图)在图中平移,直角边MN⊥BC,顶点M、N分别在边AD、BC上,延长NM到点Q,使QM=PB.若BC=10,CD=3,则当点M从点A平移到点D的过程中,点Q的运动路径长为7$\sqrt{2}$.
已知四边形ABCD,∠ABC=45°,∠C=∠D=90°,含30°角(∠P=30°)的直角三角板PMN(如图)在图中平移,直角边MN⊥BC,顶点M、N分别在边AD、BC上,延长NM到点Q,使QM=PB.若BC=10,CD=3,则当点M从点A平移到点D的过程中,点Q的运动路径长为7$\sqrt{2}$.
分析 当点P与B重合时,AM=AQ′=3$\sqrt{3}$-3,DM=DQ″=10-3$\sqrt{3}$,易知点Q的运动路径是Q′→M→Q″,△AMQ′,△MDQ″都是等腰直角三角形,由此即可解决问题.
解答 解:当点P与B重合时,AM=AQ′=3$\sqrt{3}$-3,DM=DQ″=10-3$\sqrt{3}$,
易知点Q的运动路径是Q′→M→Q″,△AMQ′,△MDQ″都是等腰直角三角形,
∵Q′M+MQ″=$\sqrt{2}$(3$\sqrt{3}$-3)+$\sqrt{2}$(10-3$\sqrt{3}$)=7$\sqrt{2}$
∴点Q的运动路径长=点P的运动路径长7$\sqrt{2}$,
故答案为7$\sqrt{2}$.
点评 本题考查平移变换、运动轨迹、解直角三角形等知识,解题的关键是理解题意,学会用转化的思想思考问题,属于中考常考题型.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
5.下列函数中不是一次函数的是( )
| A. | y=x | B. | y=2x-1 | C. | y=|x| | D. | y=1-2x |
12.已知关于x的不等式组$\left\{\begin{array}{l}{x-b≤0}\\{x-2≥3}\end{array}\right.$ 整数解有4个,则b的取值范围是( )
| A. | 7≤b<8 | B. | 7≤b≤8 | C. | 8≤b<9 | D. | 8≤b≤9 |
6. 如图所示,在矩形ABCD中,O是BC的中点,∠AOD=90°,若矩形ABCD的周长为30cm,则AB的长为( )
如图所示,在矩形ABCD中,O是BC的中点,∠AOD=90°,若矩形ABCD的周长为30cm,则AB的长为( )
 如图所示,在矩形ABCD中,O是BC的中点,∠AOD=90°,若矩形ABCD的周长为30cm,则AB的长为( )
如图所示,在矩形ABCD中,O是BC的中点,∠AOD=90°,若矩形ABCD的周长为30cm,则AB的长为( )| A. | 5 cm | B. | 10 cm | C. | 15 cm | D. | 7.5 cm |
7.反比例函数y=$\frac{k}{x}$,若k<0,则( )
| A. | y的值为负 | |
| B. | 双曲线在一、三象限 | |
| C. | y随x的增大而增大 | |
| D. | 在所在的每一个象限,y随x的增大而增大 |
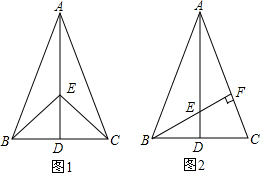
 如图,在△ABC中,BD=CD,∠1=∠2,小颖说:“AD⊥BC”,你认为她说的对吗?说明你的理由.
如图,在△ABC中,BD=CD,∠1=∠2,小颖说:“AD⊥BC”,你认为她说的对吗?说明你的理由.