题目内容
6. 如图所示,在矩形ABCD中,O是BC的中点,∠AOD=90°,若矩形ABCD的周长为30cm,则AB的长为( )
如图所示,在矩形ABCD中,O是BC的中点,∠AOD=90°,若矩形ABCD的周长为30cm,则AB的长为( )| A. | 5 cm | B. | 10 cm | C. | 15 cm | D. | 7.5 cm |
分析 首先证明△ABO≌△DCO,推出OA=OB,由∠AOD=90°,推出∠OAD=∠ODA=45°,由∠BAD=∠CDA=90°,推出∠BAO=∠CDO=45°,推出∠BAO=∠AOB,∠CDO=∠COD,推出AB=BO=OC=CD,设AB=CD=x,则BC=AD=2x,由题意x+x+2x+2x=30,解方程即可解决问题.
解答 解: ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴AB=CD,∠B=∠C=90°,
在△ABD和△DCO中,
$\left\{\begin{array}{l}{AB=DC}\\{∠B=∠C}\\{OB=OC}\end{array}\right.$,
∴△ABO≌△DCO,
∴OA=OB,
∵∠AOD=90°,
∴∠OAD=∠ODA=45°,
∵∠BAD=∠CDA=90°,
∴∠BAO=∠CDO=45°,
∴∠BAO=∠AOB,∠CDO=∠COD,
∴AB=BO=OC=CD,
设AB=CD=x,则BC=AD=2x,
由题意x+x+2x+2x=30,
∴x=5,
∴AB=5,
故选A.
点评 本题考查矩形的性质、全等三角形的判定和性质、等腰直角三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,学会构建方程解决问题,属于中考常考题型.

练习册系列答案
相关题目
11.若分式$\frac{2}{x+3}$有意义,则x的取值范围是( )
| A. | x≠-3 | B. | x≠3 | C. | x>-3 | D. | x<-3 |
15.下列调查,适合用普查方式的是( )
| A. | 调查全市初中学生的每天课外阅读时间 | |
| B. | 调查全市学生每天的睡眠时间 | |
| C. | 调查全市初中学生的视力情况 | |
| D. | 调查一个班级学生的身高 |
16.已知两圆的半径分别为1和5,圆心距为4,那么两圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
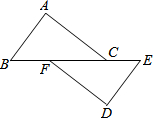 已知:如图,点B,F,C,E在一条直线上,BC=EF,AC=DF,且AC∥DF.
已知:如图,点B,F,C,E在一条直线上,BC=EF,AC=DF,且AC∥DF.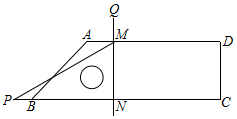 已知四边形ABCD,∠ABC=45°,∠C=∠D=90°,含30°角(∠P=30°)的直角三角板PMN(如图)在图中平移,直角边MN⊥BC,顶点M、N分别在边AD、BC上,延长NM到点Q,使QM=PB.若BC=10,CD=3,则当点M从点A平移到点D的过程中,点Q的运动路径长为7$\sqrt{2}$.
已知四边形ABCD,∠ABC=45°,∠C=∠D=90°,含30°角(∠P=30°)的直角三角板PMN(如图)在图中平移,直角边MN⊥BC,顶点M、N分别在边AD、BC上,延长NM到点Q,使QM=PB.若BC=10,CD=3,则当点M从点A平移到点D的过程中,点Q的运动路径长为7$\sqrt{2}$. 如图,二次函数的图象与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C(0,-2).
如图,二次函数的图象与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C(0,-2).