题目内容
15.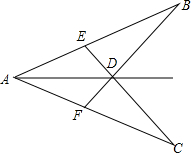 如图,AB=AC,D是∠BAC的角平分线上的一点,连结CD并延长交AB于E,连结BD并延长交AC于F,求证:AE=AF.
如图,AB=AC,D是∠BAC的角平分线上的一点,连结CD并延长交AB于E,连结BD并延长交AC于F,求证:AE=AF.
分析 先证明△BAD≌△CAD得∠B=∠C,BD=DC,再证明△BDE≌△CDF即可.
解答 证明: ∵AD平分∠BAC,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ADB和△ADC中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAD}\\{AD=AD}\end{array}\right.$,
∴△BAD≌△CAD,
∴∠B=∠C,BD=DC,
在△BDE和△CDF中,
$\left\{\begin{array}{l}{∠B=∠C}\\{BD=CD}\\{∠BDE=∠CDF}\end{array}\right.$,
∴△BDE≌△CDF,
∴BE=CF,
∵AB=AC,
∴AE=AF.
点评 本题考查全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键,本题用了两次全等,属于中考常考题型.

练习册系列答案
相关题目
7.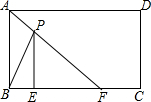 如图,在矩形ABCD中,AB=4cm,AD=5cm.点E在BC边上,且BE=1cm,AF平分∠BAD.图中P为AF上任意一点,若P为AF上任意一动点,请确定一点P,连接BP、EP,则BP+EP的最小值为( )
如图,在矩形ABCD中,AB=4cm,AD=5cm.点E在BC边上,且BE=1cm,AF平分∠BAD.图中P为AF上任意一点,若P为AF上任意一动点,请确定一点P,连接BP、EP,则BP+EP的最小值为( )
 如图,在矩形ABCD中,AB=4cm,AD=5cm.点E在BC边上,且BE=1cm,AF平分∠BAD.图中P为AF上任意一点,若P为AF上任意一动点,请确定一点P,连接BP、EP,则BP+EP的最小值为( )
如图,在矩形ABCD中,AB=4cm,AD=5cm.点E在BC边上,且BE=1cm,AF平分∠BAD.图中P为AF上任意一点,若P为AF上任意一动点,请确定一点P,连接BP、EP,则BP+EP的最小值为( )| A. | 4cm | B. | 5cm | C. | 4$\sqrt{2}$cm | D. | 3cm |
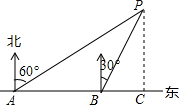 如图,小聪同学在东西走向的文一路A处,测得一处公共自行车租用服务点P在北偏东60°方向上,在A处往东90米的B处,又测得该服务点P在北偏东30°方向上,则该服务点P到文一路的距离PC为45$\sqrt{3}$.
如图,小聪同学在东西走向的文一路A处,测得一处公共自行车租用服务点P在北偏东60°方向上,在A处往东90米的B处,又测得该服务点P在北偏东30°方向上,则该服务点P到文一路的距离PC为45$\sqrt{3}$.