题目内容
7.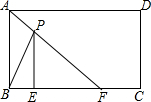 如图,在矩形ABCD中,AB=4cm,AD=5cm.点E在BC边上,且BE=1cm,AF平分∠BAD.图中P为AF上任意一点,若P为AF上任意一动点,请确定一点P,连接BP、EP,则BP+EP的最小值为( )
如图,在矩形ABCD中,AB=4cm,AD=5cm.点E在BC边上,且BE=1cm,AF平分∠BAD.图中P为AF上任意一点,若P为AF上任意一动点,请确定一点P,连接BP、EP,则BP+EP的最小值为( )| A. | 4cm | B. | 5cm | C. | 4$\sqrt{2}$cm | D. | 3cm |
分析 首先确定EB′=BP+EP的最小值,然后根据勾股定理计算.
解答 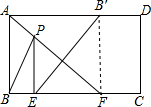 解:∵在矩形ABCD中,AF平分∠BAD.
解:∵在矩形ABCD中,AF平分∠BAD.
∴∠BAF=45°,
∴△ABF是等腰直角三角形,
作FB′⊥AD于B′,
∴四边形ABFB′是正方形,
∴B、B′关于AF对称,
连接B′E交AF于P,此时BP+EP=PB′+PE=B′E的最小值,
∵AB=4cm,AD=5cm.BE=1cm,
∴BF=B′F=4,
∴EF=4-1=3,
∴B′E=$\sqrt{E{F}^{2}+B{′F}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5cm,
∴BP+EP的最小值为5cm,
故选B.
点评 此题考查了线路最短的问题,确定动点E何位置时,使PB+PE的值最小是关键.

练习册系列答案
相关题目
15.己知函数y=(m+2)${x}^{{m}^{2}+m-4}$是关于x的二次函数.求:
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时,抛物线的开口方向、增减性如何?
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时,抛物线的开口方向、增减性如何?
16.已知⊙O外一点A到圆的最大距离为18cm,到圆的最小距离为8cm,则这个圆的半径为( )
| A. | 4cm | B. | 5cm | C. | 8cm | D. | 9cm |
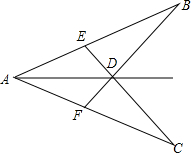 如图,AB=AC,D是∠BAC的角平分线上的一点,连结CD并延长交AB于E,连结BD并延长交AC于F,求证:AE=AF.
如图,AB=AC,D是∠BAC的角平分线上的一点,连结CD并延长交AB于E,连结BD并延长交AC于F,求证:AE=AF. 如图,锐角△ABC中,∠ABC=45°,BD是∠ABC的平分线,BC=5,E为BC上一动点,F为BD上一动点,则CF+EF的最小值为$\frac{5\sqrt{2}}{2}$.
如图,锐角△ABC中,∠ABC=45°,BD是∠ABC的平分线,BC=5,E为BC上一动点,F为BD上一动点,则CF+EF的最小值为$\frac{5\sqrt{2}}{2}$. 如图,Rt△ABO中,△AOB=90°,点A在第一象限、点B在第四象限,且AO:BO=1:$\sqrt{2}$,若已知点A在双曲线y=$\frac{1}{x}$上,点B在双曲线y=$\frac{k}{x}$上,求k的值.
如图,Rt△ABO中,△AOB=90°,点A在第一象限、点B在第四象限,且AO:BO=1:$\sqrt{2}$,若已知点A在双曲线y=$\frac{1}{x}$上,点B在双曲线y=$\frac{k}{x}$上,求k的值.