题目内容
5.若一个直角三角形的两直角边长分别为6cm和8cm,则此直角三角形斜边上高是4.8cm.分析 根据勾股定理先求出斜边,再根据面积相等,即可求出斜边上的高.
解答 解:根据勾股定理,斜边长=$\sqrt{{6}^{2}+{8}^{2}}$=10,
根据面积相等,设斜边上的高为x,则
$\frac{1}{2}$×6×8=$\frac{1}{2}$×10x,
解得,x=4.8;
故答案是:4.8.
点评 本题考查勾股定理的知识,注意利用面积相等来解题,是解决直角三角形问题的常用的方法,可有效简化计算.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
15.练习中,小明同学做了如下4道因式分解题,你认为小明做得正确的有( )
①x3+x=x(x+1)(x-1);
②x2-2xy+y2=(x-y)2;
③a2-a+1=a(a-1)+1;
④x2-16y2=(x+4y)(x-4y).
①x3+x=x(x+1)(x-1);
②x2-2xy+y2=(x-y)2;
③a2-a+1=a(a-1)+1;
④x2-16y2=(x+4y)(x-4y).
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.下列各组数据分别是三角形的三边长,其中不能构成直角三角形的是( )
| A. | 2,4,2$\sqrt{3}$ | B. | 1,1,$\sqrt{2}$ | C. | 1,2,$\sqrt{5}$ | D. | $\sqrt{3}$,2,$\sqrt{5}$ |
14. 如图,AD是△ABC的中线,E是AD中点,BE的延长线与AC交于点F,则AF:AC等于( )
如图,AD是△ABC的中线,E是AD中点,BE的延长线与AC交于点F,则AF:AC等于( )
 如图,AD是△ABC的中线,E是AD中点,BE的延长线与AC交于点F,则AF:AC等于( )
如图,AD是△ABC的中线,E是AD中点,BE的延长线与AC交于点F,则AF:AC等于( )| A. | 1:2 | B. | 2:3 | C. | 1:3 | D. | 2:5 |
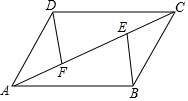 如图,E,F是四边形ABCD的对角线AC上点,AF=CE,DF=BE,DF∥BE.
如图,E,F是四边形ABCD的对角线AC上点,AF=CE,DF=BE,DF∥BE.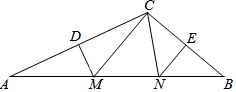 如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N,
如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N, 如图:点P是线段AB上任意一点,且C、D分别为线段AP、BP的中点,若CD=5cm,则有AB=10cm.
如图:点P是线段AB上任意一点,且C、D分别为线段AP、BP的中点,若CD=5cm,则有AB=10cm. 如图,△ABC的顶点都是正方形网格中的格点,则tan∠ABC=$\frac{1}{2}$.
如图,△ABC的顶点都是正方形网格中的格点,则tan∠ABC=$\frac{1}{2}$.