题目内容
17. 如图:点P是线段AB上任意一点,且C、D分别为线段AP、BP的中点,若CD=5cm,则有AB=10cm.
如图:点P是线段AB上任意一点,且C、D分别为线段AP、BP的中点,若CD=5cm,则有AB=10cm.
分析 根据线段中点的性质,可得AP,PB,根据线段的和差,可得答案.
解答 解:由C、D分别为线段AP、BP的中点,得
AP=2CP,PB=2PD.
由线段的和差,得
AB=AP+PB=2(CP+PD)=2CD=10,
故答案为:10cm.
点评 本题考查了两点间的距离,利用线段中点的性质得出AP=2CP,PB=2PD是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.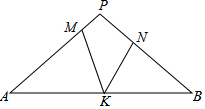 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为( )
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为( )
 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为( )
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为( )| A. | 44° | B. | 66° | C. | 96° | D. | 92° |
9.已知cosα=0.8391,cotβ=0.5774,则锐角α,β的大小关系是( )
| A. | α>β | B. | α≤β | C. | α<β | D. | α=β |
6. 如图,在2×2的正方形网格中,每个小正方形边长为1,点A,B,C均为格点,以点A为圆心,AB长为半径作弧,交格线于点D,则CD的长为( )
如图,在2×2的正方形网格中,每个小正方形边长为1,点A,B,C均为格点,以点A为圆心,AB长为半径作弧,交格线于点D,则CD的长为( )
 如图,在2×2的正方形网格中,每个小正方形边长为1,点A,B,C均为格点,以点A为圆心,AB长为半径作弧,交格线于点D,则CD的长为( )
如图,在2×2的正方形网格中,每个小正方形边长为1,点A,B,C均为格点,以点A为圆心,AB长为半径作弧,交格线于点D,则CD的长为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\sqrt{3}$ | D. | 2-$\sqrt{3}$ |
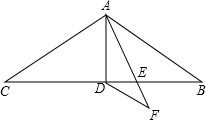 如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为( )
如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为( ) 如图,直线a∥b,∠3=85°,求∠1、∠2的度数,根据下面的解答过程,填空或填写理由.
如图,直线a∥b,∠3=85°,求∠1、∠2的度数,根据下面的解答过程,填空或填写理由.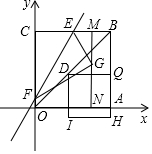 如图,四边形OABC是一张放在平面直角坐标中的正方形纸片,点O与坐标原点重合,点A 在x轴上,点C在y轴上,OC=4,点E为BC的中点,点N的坐标为(3,0),过点 N且平行于y轴的直线MN与EB交于点M.现将纸片折叠,使顶点C落在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.连接OB,D为OB上动点,作DQ∥x轴交BA于点Q,以DQ为边,向下作正方形DQHI,设点D的横坐标为t.
如图,四边形OABC是一张放在平面直角坐标中的正方形纸片,点O与坐标原点重合,点A 在x轴上,点C在y轴上,OC=4,点E为BC的中点,点N的坐标为(3,0),过点 N且平行于y轴的直线MN与EB交于点M.现将纸片折叠,使顶点C落在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.连接OB,D为OB上动点,作DQ∥x轴交BA于点Q,以DQ为边,向下作正方形DQHI,设点D的横坐标为t.