题目内容
16. 如图所示,已知AB⊥FC于B,DE⊥FC于E,AB,DF交于M,AC,DE交于N,BF=CE,AC=DF.求证:∠A=∠D.
如图所示,已知AB⊥FC于B,DE⊥FC于E,AB,DF交于M,AC,DE交于N,BF=CE,AC=DF.求证:∠A=∠D.
分析 根据等式的性质得出FE=BC,再利用全等三角形的判定得出△ABC与△DEF全等,证明即可.
解答 证明:∵BF=CE,
∴BF+BE=CE+BE,
即EF=BC,
∵AB⊥FC于B,DE⊥FC于E,
在RT△ABC与RT△DEF中,
$\left\{\begin{array}{l}{AC=DF}\\{EF=BC}\end{array}\right.$,
∴RT△ABC≌RT△DEF(HL),
∴∠A=∠D.
点评 此题考查全等三角形的判定和性质,关键是根据等式的性质得出FE=BC,再利用全等三角形的判定得出△ABC与△DEF全等.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
4.某次知识竞赛共计25道题,评分标准如下:答对1题加4分,答错1题扣1分,她的总分为75分,则她答对了( )
| A. | 18题 | B. | 19题 | C. | 20题 | D. | 21题 |
5.我市园林管理部门对去年栽下的A、B、C、D四个品种的树苗进行了成活率抽样统计,以下时根据抽样统计数据制成的不完整的统计表和统计图:
栽下的各品种树苗棵数统计表

已知C种树苗的成活率为92%.根据以上信息解答下列问题:
(1)本次抽样统计中的四个品种的树苗共多少棵?
(2)求本次抽样统计中C种树苗的成活棵数,并补全条形统计图.
(3)若去年我市栽下四个品种的树苗共计5000棵,请估计这些树苗中B种树苗成活的棵树.
栽下的各品种树苗棵数统计表
| 植树品种 | A种 | B种 | C种 | D种 |
| 植树棵数 | 150 | 125 | 125 |

已知C种树苗的成活率为92%.根据以上信息解答下列问题:
(1)本次抽样统计中的四个品种的树苗共多少棵?
(2)求本次抽样统计中C种树苗的成活棵数,并补全条形统计图.
(3)若去年我市栽下四个品种的树苗共计5000棵,请估计这些树苗中B种树苗成活的棵树.
6.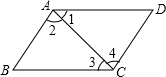 如图,在四边形ABCD中,要得到AB∥CD,只需要添加一个条件,这个条件可以是( )
如图,在四边形ABCD中,要得到AB∥CD,只需要添加一个条件,这个条件可以是( )
 如图,在四边形ABCD中,要得到AB∥CD,只需要添加一个条件,这个条件可以是( )
如图,在四边形ABCD中,要得到AB∥CD,只需要添加一个条件,这个条件可以是( )| A. | ∠1=∠3 | B. | ∠2=∠4 | C. | ∠B=∠D | D. | ∠1+∠2+∠B=180° |
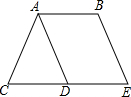 在平行四边形ABED中,CD为DE延长线,连接AC,AD恰好为∠BAC角平分线,且∠BAD=60°,BE=2cm,求△ACD的周长.
在平行四边形ABED中,CD为DE延长线,连接AC,AD恰好为∠BAC角平分线,且∠BAD=60°,BE=2cm,求△ACD的周长. 如图所示,点A,B,C,D在同一直线上,AB=CD,∠D=∠ECA,EC=FD,求证:AE=BF.
如图所示,点A,B,C,D在同一直线上,AB=CD,∠D=∠ECA,EC=FD,求证:AE=BF.